I Electric Potential in circuit

[eyeweyew]

TL;DR Summary

Electric potential at a point equation for circuit and net charge

I reviewed some of the fundamental physics and I looked back at the equation for Electric potential at a point p:
$$V(p) = k \sum_{i} {\frac {q_i} {r_i}}$$
where

- p is the point at which the potential is evaluated;
- r_i is the distance between point p and point i at which there is a nonzero charge;
- q_i is the charge at point i

and I still find it's kind of contradicting with the simple circuit model such as the one below. Both point a and point b should be neutral with no net charge so their electric field is 0 and the voltage is flat on the graph according to Gauss law. I understand the electric potential of point b is ε higher than that of point a (i.e. V(b)-V(a)=ε) means it takes ε work to move a +1 test charge from point a to point b along the circuit.

But according to Electric potential formula at a point, should that also imply there are higher positive net charge concentration around point b than point a so how can they both neutral with no net charge? Does that mean the equation for Electric potential at a point does not apply in a circuit model but if so, why?

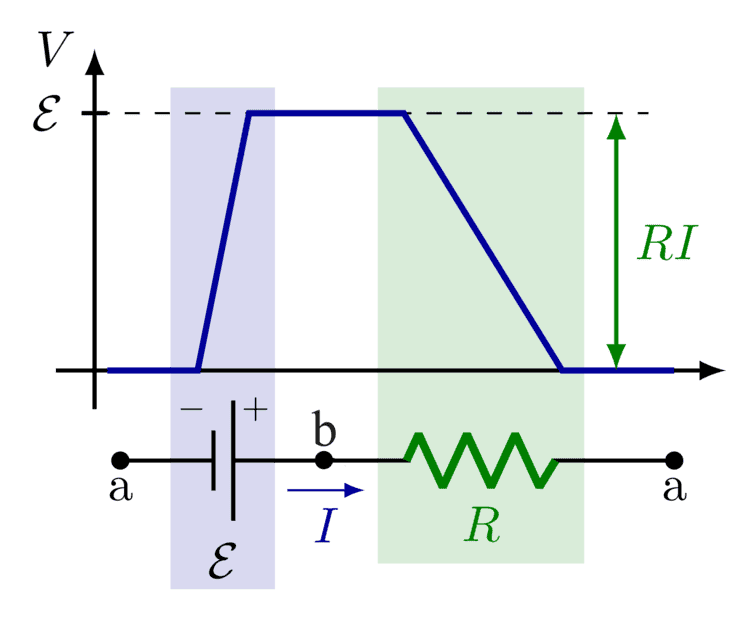
image reference: https://tikz.net/electric_circuit_voltage_plots/

 

[Dale]

Is that formula supposed to be the voltage at a point or the voltage due to a point charge? Read the surrounding text carefully

 

[eyeweyew]

Is that formula supposed to be the voltage at a point or the voltage due to a point charge? Read the surrounding text carefully

It is voltage at a point due to other point charges. I edited my post to clarify it. Thanks!

 

[Dale]

It is voltage at a point due to other point charges. I edited my post to clarify it. Thanks!

So that formula doesn’t really apply. There are no solitary point charges in that circuit. There is a continuous distribution of surface charge along all the conductors. That distribution doesn’t have a nice closed form expression.