Electrical Energy Dissipation Across Resistors

Click For Summary

Homework Help Overview

The discussion revolves around electrical energy dissipation across resistors in a circuit, specifically focusing on calculating power dissipation in resistors and the power output of batteries. The problem involves understanding voltage differences, current, and resistance in a series circuit.

Discussion Character

  • Exploratory, Assumption checking, Problem interpretation

Approaches and Questions Raised

  • Participants discuss how to determine voltage differences and the implications of resistor values. There are attempts to calculate current and power using given equations, but confusion arises regarding the correct application of these concepts.

Discussion Status

Some participants have provided guidance on summing voltages and resistances to find current, while others are questioning the accuracy of the calculations and the direction of voltages. Multiple interpretations of the problem setup are being explored, indicating an ongoing dialogue without a clear consensus.

Contextual Notes

There is mention of an attached image that may contain crucial information for solving the problem, but its content is not described in the posts. The original poster expresses uncertainty about the voltage drop and the meaning of resistor values, indicating potential gaps in understanding the circuit configuration.

Yosty22
Messages
182
Reaction score
4

Homework Statement



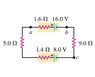
(image attached)
A). What is the total rate at which electrical energy is dissipated in the 5.0−Ω resistor?
B). What is the total rate at which electrical energy is dissipated in the 9.0−Ω resistor?
C). What is the power output of the 16.0-V battery?
D). At what rate is electrical energy being converted to other forms in the 8.0-V battery?


Homework Equations



P=V_ab(I)=I^2R=V_ab^2/R

The Attempt at a Solution



I can't figure this out at all. For part A, I need the voltage difference and the resistance. How would I find the voltage difference? And does the 5 ohm resistor mean that the resistance is 5 over the resistor? In which case I need to find the voltage drop across the resistor. How do I do this?
 
Physics news on Phys.org
no image attached
 
  • Like
Likes   Reactions: 1 person
Sorry, attached it now!
 

Attachments

  • YF-25-48 (1).jpg
    YF-25-48 (1).jpg
    6.6 KB · Views: 1,100
Just sum up all of the voltage sources around the loop and all the resistances, since they're all in series, and you'll have the current around the loop. Can you take it from there?
 
Ok, so I added up the voltages (24V) and added up the resistance (17 ohms). I then did V/R to get I=1.412A. Then, I used the equation P=V_ab * I and got P=120W, but it is wrong. What am I doing here?
 
You are not taking into account the direction of the voltages.
 

Similar threads

Graphing the Power dissipated in a resistor
  • · Replies 1 ·
Replies
1
Views
2K
Energy dissipated in a resistor
  • · Replies 16 ·
Replies
16
Views
3K
Energy dissipated by resistor problem
  • · Replies 3 ·
Replies
3
Views
3K
Calculating the voltage across capacitors and resistors with switches
  • · Replies 2 ·
Replies
2
Views
1K
What Is the EMF of a Cell with Given Energy Dissipation and Current?
  • · Replies 4 ·
Replies
4
Views
5K
Rank Resistors by Energy Dissipation: 5Ω > 10Ω > 20Ω > 90Ω
  • · Replies 4 ·
Replies
4
Views
2K
Joule heating effect - qualitative explanation
  • · Replies 8 ·
Replies
8
Views
2K
Electric Potential across charging battery.
  • · Replies 5 ·
Replies
5
Views
2K
RC Circuit - Rate energy is dissipated in the resistor
  • · Replies 4 ·
Replies
4
Views
3K
Total rate at which electrical energy is dissipated by resistors
  • · Replies 6 ·
Replies
6
Views
9K