Electrical forces between two beads in a hemisphere

[Nick O]

Homework Statement

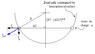
Two identical beads each have a mass m and charge q. When placed in a hemispherical bowl of radius R with frictionless, nonconducting walls, the beads move, and at equilibrium, they are a distance d apart. a) Determine the charge q on each bead. b) Determine the charge required for d to become equal to 2R.

[See image]
https://www.physicsforums.com/attachments/61123

Homework Equations

Electric force $\vec{F}_{e}=k_{e}\frac{q^{2}}{d^{2}}\hat{r}$

Gravitational force = $-mg\hat{j}$

Normal force = $\vec{n}$
$|\vec{n}|cos(θ) = |\vec{F}_{e}|$
$|\vec{n}|sin(θ) = mg$

... where θ is the angle between the normal force and the horizonal.

The Attempt at a Solution

The normal force equations above sum up my progress toward solving the problem. I believe that I somehow need to find the normal force in order to solve for the electric force, which I need in order to solve for q. But, to solve for the normal force, I need to solve for θ, and here I am stuck; I have two equations and three unknowns.

I feel that knowing the lengths of all three sides of the isosceles triangle formed by the center of the hemisphere and the two beads is significant, but I can't find any connection between the angles in that triangle and the angle of the normal force.

With that, I am at your mercy. Any guidance would be much appreciated.

4. Vaguely human introduction.

Hello! I am currently taking Physics II (a calculus-based course with a focus on electromagnetism), and am working toward BS in Computer Engineering. The problem above is, of course, homework. As such, I'm sure we can all agree that the most I should be given is a nudge in the right direction, and not the actual answer.

Thank you in advance.

5. Forum bug discovered.

Whenever I click "Preview Post", the post template is pasted at the end of the message box. To see what I mean, scroll down.

Homework Statement

Homework Equations

The Attempt at a Solution

 

[TSny]

Hello, NickO. Welcome to PF.

Everything you've done looks very good to me. And I think you are right that you need to find another relationship using geometry. What if you drop a perpendicular line from the center of the sphere to the base of your isosceles triangle?

 

[Nick O]

Thank you for the quick response and warm welcome!

Your response confirms my gut feeling - the normal force does follow the radius of the circle. The reason for my doubt was that I had forgotten, over the course of the summer, that normal forces are always perpendicular the the contact surface. In my mind, the normal force could have been pointing in any direction so long as it balanced the free-body diagram.

Thank you very much!

 

[gneill]

Hi Nick O.

Your attachment "Attachment 61123" does not seem to work (at least not for me). Assuming that I've correctly interpreted your text, the following diagram should depict the situation:

Note that you should be able to avoid trig functions if you use similar triangles (geometry) instead...

 

[Nick O]

Odd, it doesn't work for me, either. Your diagram accurately depicts the problem.

Thank you both!

 

[Nick O]

As a way to check my calculations on the problem, is the answer to part B as follows? "Infinite charge is required for d to equal 2R."

 

[TSny]

As a way to check my calculations on the problem, is the answer to part B as follows? "Infinite charge is required for d to equal 2R."

Yes, that's correct.

 

[Nick O]

Thank you once more. I appreciate it!