Electromagnetic Tensor in (-+++) Convention

[tomdodd4598]

Hi there,

Over the last couple of weeks, I have been learning about the relativistic description of electromagnetism through Leonard Susskind's Theoretical Minimum lectures, and although I have managed to follow it, there are some parts which I am becoming increasingly confused by, not helped by the fact Susskind uses the (-+++) convention rather than the seemingly more popular (+---).

Is the definition of the electromagnetic tensor different depending on the convention? I am aware that the matrix changes (the contravariant and covariant forms are multiplied by -1 when moving between conventions), but does the definition of each component in terms of the vector potential change?

The reason I ask this is because when deriving the relativistic Lorentz force from the Lagrangian:
L=-m√(-dX_ϑ/dt dX^ϑ/dt)-qA_ϑ dX^ϑ/dt
I always seem to get the following answer (using the (-+++) convention):

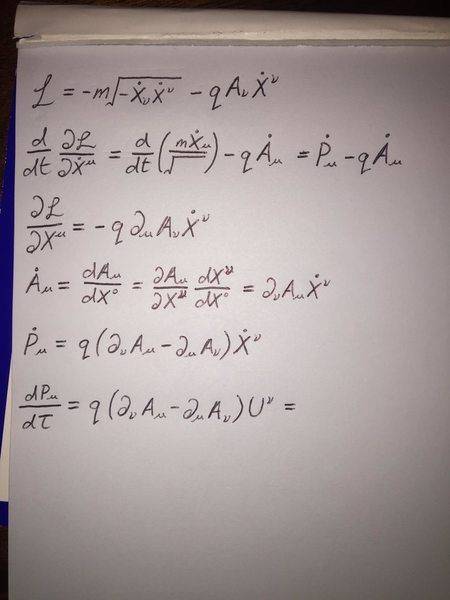
Which is the negative of what I would expect from the definition of the Electromagnetic Tensor.

Any help would be appreciated, and thanks in advance.

 

[Jilang]

Yes. Here is discussion on the subject.
http://physics.stackexchange.com/qu...-the-definition-of-the-electromagnetic-tensor

 

[robphy]

Note that there are also conventions regarding the index structure of F...
the ;-notation vs the ∇-notation.

 

[tomdodd4598]

Maybe the Lagrangian should be:
L=-m√(-dX_ϑ/dt dX^ϑ/dt)+qA_ϑ dX^ϑ/dt
when using the (-+++) convention?