Electrostatics - Electric field of a quadrupole

[AwesomeTrains]

Homework Statement

Hello PF,
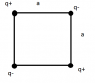
I could use some help calculating the electric field of a static quadrupole with side lengths a. The four charges are each placed in the corners of a square. (See attached picture).

Homework Equations

We've been given these as a help:
\Phi_{Q}(\vec{r})=\vec{a}\cdot\nabla\Phi_{D}+O(\left|\vec{a}^{3}\right|) Were O(\left|\vec{a}^{3}\right|) can be left out.

And \Phi_{D}(\vec{r})=\frac{1}{4\pi\epsilon_{0}}\frac{\vec{p}\cdot\vec{r}}{r^{3}}
Were \vec{p}=q\cdot\vec{d} is the dipole moment, q is the charge and \vec{d} is the distance vector.

The Attempt at a Solution

\Phi_{Q} is the potential of the quadrupole. Therefore I thought I could plug in \Phi_{D} and then use Gauss's law \vec{E}=-\nabla\Phi_{Q}
But how do I do that? I have problems using nabla on that function, and \vec{d}, \vec{a} confuses me. (Are they the same?)
Any hints are very appreciated :)

 

[Solibelus]

My suggestion: to understand this properly you should derive the potential generally using the definition of potential at some point P (apply binomial expansion for some configuration of charge).
Afterwards do some algebra with the terms and get Legendre polynomials as coefficients. Your quadrupole will be represented by the third term. A dipole will be the second term etc.
Start with a dipole and generalize from there, it's not as difficult as it sounds and you must've done it in class at some point.
After developing the general expression you will be able to use it in any case, quadrupoles, octopoles or whatever.

I looked at my course notes and they're very similar to David J. Griffiths' Introduction to Electrodynamics, so you should take a peek there for clues.

 

[AwesomeTrains]

Thanks for the help. Will try and give it a shot :)
I have never heard of the multipole expansion before neither Legendre polynomials. I have only been studying physics for nearly a year now. And we haven't done that in class yet.