Energy conservation in destructive interference.

[siddharth5129]

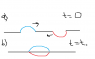
I have followed some of the previous posts on the topic , but the conflicting arguments have left more than confused. Consider this simple scenario : Two wave pulses on a string generated by identical sources but with a phase difference of 180 degrees meet and interfere destructively. For simplicity, let's assume that their amplitudes are the same. Where does the energy of the two wave pulses ( 2*Asquared ) go in the moment when the amplitude of the disturbance on the string is zero. Possible explanations I have received for this are :

1) The energy is absorbed by the source.
2) Stored in the potential energy of the string as it is disturbed by two displacements in the opposite sense.
3) Energy is not a local property , and it remains conserved over time in this case ( after the waves separate )

Personally, I find the second argument the most appealing, but I'd like to be sure ... which is it?
Any help would be greatly appreciated.

 

[olivermsun]

The A^2 dependence is based on the amplitude of the oscillation, e.g., y = A cos ft. You can see from this that y = 0 for some instants t, but the amplitude of the oscillation is not 0 at those times. The other thing you can realize is that the string is actually moving (it has kinetic energy) at the moment it crosses zero. The same thing applies when there are two superposed oscillations, e.g., y = A cos ft + B cos gt.

The question about the two out-of-phase impulses is a little diffferent. If you were actually to start two identical impulses at the same point on the string with exactly opposite sign, then wouldn't you have no impulse at all?

 

[siddharth5129]

Lets assume that the two out of phase impulses are generated at two opposite ends of a string. My question then would be , where does the energy go in the instant that the resulting wave amplitude turns zero.

 

[Jano L.]

Hi there,
say two same Gaussian pulses of opposite amplitude would be traveling towards each other. In the center they will cancel each other and the string will be at rest all the time due to symmetry. But all the other points of the string, although they all will be at equilibrium position when two pulses are eclipse, will not be at rest, but would move up or down according to which pulse is stronger at this position. So the energy has to be stored in the kinetic energy of the string.
Best wishes,
Jano

 

[nasu]

Lets assume that the two out of phase impulses are generated at two opposite ends of a string. My question then would be , where does the energy go in the instant that the resulting wave amplitude turns zero.

At that instant the particles of the string have nonzero velocities. So all the energy is kinetic energy. A little similar with asking where is the energy of an oscillator at the instant the spring is not deformed (equilibrium position).
After the instant in question the string continues to oscillate and the two waves move toward the ends, right?

 

[siddharth5129]

"At that instant the particles of the string have nonzero velocities."
I'm sorry but I think I've missed something important here. Don't the particles have zero velocities at that instant. It's two wave pulses in opposite phase exactly superimposed on one another, so it would seem that the particles do, in fact, possesses zero velocities at that instant.

 

[xts]

If you pull your string on opposite ends, the interference is not destructive (the pulses are not opposite phase exactly superimposed on one another).

If you pull the string in the same place (one end) with two forces, equal to the magnitude, but of opposite signs - then the resulting force is always zero, string does not vibrate, but also the energy transfer is zero - forces do not perform any work, they just cancel each other.

 

[siddharth5129]

Well ... I'm not sure what you are getting at. Anyway, to be clear, the scenario that I have drawn out on the attachment is what I am trying to convey. At time t = 0 , the string has a finite amount of energy , and at time t = t1 , The energy of the string is suddenly zero. ( assuming amplitudes of the red and blue waves to be the same. In part b) , the black line is the resultant amplitude ) Where does this energy go ?

 

[olivermsun]

Well ... I'm not sure what you are getting at. Anyway, to be clear, the scenario that I have drawn out on the attachment is what I am trying to convey. At time t = 0 , the string has a finite amount of energy , and at time t = t1 , The energy of the string is suddenly zero. ( assuming amplitudes of the red and blue waves to be the same. In part b) , the black line is the resultant amplitude ) Where does this energy go ?

In your picture, the places where the center of the blue pulse has passed (to its left) are moving downward (returning to center). Similarly, the places where the center of the red pulse has passed (to its right) are moving upward. At the moment b) where they pulses overlap and cancel, the parts of the string near the left edge of the overlap are still moving downward and the parts near the right edge of the overlap are still moving upward. The energy of the string never goes to zero.

 

[nasu]

"At that instant the particles of the string have nonzero velocities."
I'm sorry but I think I've missed something important here. Don't the particles have zero velocities at that instant. It's two wave pulses in opposite phase exactly superimposed on one another, so it would seem that the particles do, in fact, possesses zero velocities at that instant.

It was already answered by the other posters.
Just to specify a little more, the speed is zero only in the center of the string. The other parts of the string have non-zero velocities. If the velocity were zero everywhere (and the string being in the equilibrium position) there will be no further motion and no waves going propagating toward the ends of the string.

 

[JeffKoch]

Where does this energy go ?

I think you already have the answer if you read the posts above. It never went anywhere.

 

[siddharth5129]

It was already answered by the other posters.
Just to specify a little more, the speed is zero only in the center of the string. The other parts of the string have non-zero velocities. If the velocity were zero everywhere (and the string being in the equilibrium position) there will be no further motion and no waves going propagating toward the ends of the string.

Ok, just to be clear, when you say that the speed is zero only in the centre of the string, you mean the central region where the wave pulses completely cancel each other out right, because I just don't see how particles anywhere in that region could possesses a non-zero velocity.
And further, for clarity, in reference to olivermsun's post, am I correct in inferring then that the energy of the progressive wave pulse comes only from the particles to the immediate left and right of the wave pulse, which are either moving up or down depending on the shape and direction of wave travel. That would make a whole lot of sense then.

Thanks for all the replies, greatly appreciated and extremely helpful.

 

[nasu]

Ok, just to be clear, when you say that the speed is zero only in the centre of the string, you mean the central region where the wave pulses completely cancel each other out right, because I just don't see how particles anywhere in that region could possesses a non-zero velocity.

No, I mean the central point not the central region. The velocity of the string at a given time is a function of position, v(x).
It is zero for a specific value of x, (let's say x=xm, the middle point) and non zero for the points around xm. Of course, if the cord is long compared with the pulse widths the speed will be also zero for points far away from the pulses.
You can do it yourself. "Take" two identical Gaussian pulses (easy to calculate) that propagate in opposite directions, add them to get the total displacement and take the time derivative to calculate the distribution of the speed in the cord at any time, including at the time you are interested in.

Here is an example of a possible velocity distribution at the moment in question. The two pulses start from the x=0 and x=10 m and propagate with velocities of 1m/s. They meet in the center at x=5m at t=5s.
The plot represents v(x) at t=5 s.

 

[olivermsun]

And further, for clarity, in reference to olivermsun's post, am I correct in inferring then that the energy of the progressive wave pulse comes only from the particles to the immediate left and right of the wave pulse, which are either moving up or down depending on the shape and direction of wave travel. That would make a whole lot of sense then.

There's also potential energy due to stretching in the string. In any segment where the string has a slope/tilt, it has to span a long distance than if it were lying horizontal. Just as in the case of a spring, the stretched part is under greater tension than the unstretched bits, and this is where the potential energy comes from.

But yes, as you point out each segment of string is connected to the bits on either side, so if one bit of string starts moving up or down, you might expect the neighboring bits to be affected as well.

 

[Dale]

You can do it yourself. "Take" two identical Gaussian pulses (easy to calculate) that propagate in opposite directions, add them to get the total displacement and take the time derivative to calculate the distribution of the speed in the cord at any time, including at the time you are interested in.

To expand on this, in units where the speed of the wave is 1 you can write the equation of a wave moving to the right as:
$$f(x-t)$$
and a wave moving to the left as:
$$g(x+t)$$
In order to achieve complete destructive interference at t=0 we find:
$$g(x)=-f(x)$$

Then computing the velocity we find:
$$\frac{df}{dt}=-f'(x-t)$$
$$\frac{dg}{dt}=-f'(x+t)$$

So at t=0 (complete destructive interference) we find that the velocity adds constructively:
$$\frac{d(f+g)}{dt}\bigg|_{t=0}=-2f'(x)$$