Eduardo Leon
- 6
- 0
Homework Statement
Hi mates, I have problems solving the third part of this exercise, I've already done all the previous calculations.
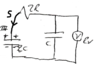
Given the following circuit, where the switch S is open, the power supply = 50 volts and:
- The initial charge in the C capacitor: QC = 0 coulombs
- The initial charge in the 2C capacitor: Q2C = 20^-6 coulombs
- Switch⇒I find the current passing by the amperemeter (IA) and the voltage across the voltmeter VV After a long time t (t>5 time constants). (Done).
- Switch⇒II find the voltage across the voltmeter VV passed 10 milliseconds. (Done).
- Switch⇒III next get the final reading of the voltmeter VV at a given time t (t >0 ∧ t< 5 time constants) and the energy dissipated in the resistors till that instant.
Homework Equations
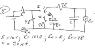
- Ohm's law: R=ΔV/i
- Capacitance: C=q/ΔV
- Kirchoff's laws: Σi=0 ∧ ΣΔV=0
- Energy gived by the battery until an instant t
- Energy dissipated in the resistor until an instant t
- Energy stored in the capacitor until an instant t
The Attempt at a Solution
As stated before, I've done the first and the second parts.
For the first:
- Amps*
- Volts*
- ⇒⇒Volts*
Well, here is where i get lost, because I dont't know how to study and analize the circuit formed at this point, I've only seen discharging RC circuits whis a single current, one resistor and one capacitor due those elements could be joined into their equivalent ones, but here, I get 2 resistors, 2 capacitors and 2 meshes, like this one.
I know that the initial charges at this point are:
In order to get the initial charge in the C capacitor I used the voltage obtained in the voltmeter in the second part at the 10 milliseconds, because are connected parallel. So, multiplying that voltage times the capacitance, we get
Attachments
-
 33333333333333.png19.6 KB · Views: 398
33333333333333.png19.6 KB · Views: 398 -
 attachment.jpg30.4 KB · Views: 774
attachment.jpg30.4 KB · Views: 774 -
 Image1.gif621 bytes · Views: 559
Image1.gif621 bytes · Views: 559 -
 Image2.gif666 bytes · Views: 544
Image2.gif666 bytes · Views: 544 -
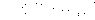 Image3.gif624 bytes · Views: 564
Image3.gif624 bytes · Views: 564 -
 58_59e4a5e4c7a317067e0e748d4c7303e8.png1.2 KB · Views: 535
58_59e4a5e4c7a317067e0e748d4c7303e8.png1.2 KB · Views: 535 -
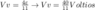 55_39ed5ab39f3e1b932d58b8143acf9655.png1 KB · Views: 537
55_39ed5ab39f3e1b932d58b8143acf9655.png1 KB · Views: 537 -
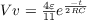 49_549e15a8fc3c64f775b461c0ce4c83f2.png870 bytes · Views: 520
49_549e15a8fc3c64f775b461c0ce4c83f2.png870 bytes · Views: 520 -
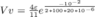 73_a3a7a2e80e63986351b15fb412bb6203.png981 bytes · Views: 570
73_a3a7a2e80e63986351b15fb412bb6203.png981 bytes · Views: 570 -
 34_76bab7f98db551c5bfbe82b73004a907.png1.2 KB · Views: 606
34_76bab7f98db551c5bfbe82b73004a907.png1.2 KB · Views: 606 -
 49_f93ffa7bf895f1ac07d8dc5df756a1e0.png1.3 KB · Views: 593
49_f93ffa7bf895f1ac07d8dc5df756a1e0.png1.3 KB · Views: 593
Last edited by a moderator: