Energy equation for fluid mechanics

[TimeRip496]

Homework Statement

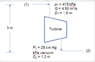
Water is supplied at 4.50 m³/s and 415 kPa (abs) to a hydraulic turbine through a 1.0-m inside diameter inlet pipe as indicated in the figure. The turbine discharge pipe has a 1.2-m inside diameter. The static pressure at section (2), 3 m below the turbine inlet, is 25 cm Hg vacuum. If the turbine develops 1.9 MW, determine the power lost between sections (1) and (2). (ANS:290kW)

Homework Equations

$${\displaystyle {{\frac {v_1^{2}}{2}}+gz_1+{\frac {p_1}{\rho }}=\frac {v_2^{2}}{2}}+gz_2+{\frac {p_2}{\rho }}+h_{shaft}+h_{lost}={\text{constant}}}$$

The Attempt at a Solution

To find the velocity,
$$v_1=4.50÷(0.5^2 \pi)=5.73 m/s $$
$$v_2=4.50÷(0.6^2 \pi)=3.98 m/s $$

Apply energy equation,
$$415(10^3) + 0.5\rho_w (5.73^2)+\rho_w g(3) = 1.9(10^6)÷4.5 +\frac{25}{76}(1.01*10^5)+0.5\rho_w (3.98^2)+P_{lost}÷4.5 $$ $$ P_{lost}=4.5(460846.45-463366.12)=-11338.515$$

However this is not possible as the power lost must be positive based on the above formulated steps. Besides the answer is not the same as the correct answer which is 290kW.

 

[jackwhirl]

...
The static pressure at section (2), 3 m below the turbine inlet, is 25 cm Hg vacuum.
...

You've got a sign error.

 

[TimeRip496]

You've got a sign error.

Shouldn't 25cm Hg vacuum means 25cm Hg above vacuum pressure which is zero? Why is 25cm Hg vacuum equivalent to 25cm Hg below atm?

 

[jackwhirl]

Shouldn't 25cm Hg vacuum means 25cm Hg above vacuum pressure which is zero? Why is 25cm Hg vacuum equivalent to 25cm Hg below atm?

Because the first interpretation is the same as absolute pressure, in which case there's no need to differentiate. But the problem statement calls it out both ways, abs and vacuum.

That and convention, I suppose.

 

[Chestermiller]

25 cm vacuum means 51 cm absolute pressure.

 

[TimeRip496]

Okay thanks! Was really confused by the terms given