Energy levels of helium/equation

[granpa]

the equation for the energy levels of a hydrogen-like atom is:

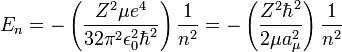
Note that a_μ, is approximately equal to a₀, (the Bohr radius). If the mass of the nucleus is infinite then μ = m_e, and a_μ = a₀

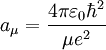
but what is the equation for the energy levels of a helium or helium-like atom? I've heard that heliums spectrum is simply 2 hydrogen spectrums superimposed so it should be quite simple.

 

[malawi_glenn]

as far as I know, you can't solve those system exactly. Only two-body systems can be

 

[granpa]

I'm not asking for a 'solution'. I'm asking what equation fits the empirically observed spectrum.

 

[Vanadium 50]

But that's what a solution is.

 

[granpa]

I'm not even going to touch that.

 

[f95toli]

So what ARE you asking for then?
Are you asking if there is e.g. an interpolating polynomial (or more realistically; an expansion using some other bases; e.g. Lorentzians) that fits the shape of an experimental spectrum?

I doubt such a thing exist; it is of course possible to create but it would need to contain so many terms that it would be useless; it is much easier to look up the data in a table or just run a computer simulation.

 

[Redbelly98]

In practice, as far as I know, people either look up the energy levels from a table or chart, OR they run computer simulations to calculate them.

For the simulations, you might do a search on Gordon W. F. Drake. He practically made a living from accurate calculations of helium, at least in the 1990's. Three references to his work are given here:

http://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable7.htm

EDIT: Understanding Drake's calculations in any detail pretty much requires grad-school level quantum mechanics.

 

[granpa]

thank you. that was extremely helpful.