Entropy change when the number of particles decreases

[greypilgrim]

Hi.

I found following exercise in a high school textbook:
"Compute the entropy change in following process:"

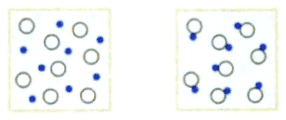
The solution is
"The number of particles decreases from $N_1$ to $N_2=N_1/2$. Hence the entropy decreases by
$$\Delta S=-k\cdot N_1\cdot \ln{2}\enspace ."$$

I can't quite follow the argument here. Assuming the particles in each picture are non-interacting and have the same number of microstates $\Omega$, I get
$$S_1=N_1\cdot k\cdot \ln{\Omega}$$
$$S_2=N_2\cdot k\cdot \ln{\Omega}=\frac{N_1}{2}\cdot k\cdot \ln{\Omega}=\frac{S_1}{2}$$
from which I can see that the entropy decreases, but cannot compute the difference since I don't know $\Omega$.

 

[DrDu]

I have doubts that the exercise makes much sense. E.g. if this is meant to be a chemical reaction in an isolated container, the system will heat up and entropy will increase rather than decrease.