Equation for modeling atomic spectra of all atoms

[Xilus]

I've seen the equation I think is just for hydrogen. is this just for hydrogen?

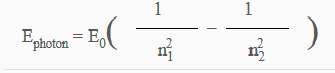
of course this doesn't return the atomic spectra, it returns the energy.
So using E=h*v and Planck's constant. a simple factor of 1/h would return the frequency.
right? Energy is directly proportional to frequency.
and E0=13.6eV n1<n2 where both n1 and n2 are integers

Is there an equation that models atomic spectra of all atoms?

 

[blue_leaf77]

is this just for hydrogen?

Yes it's only for hydrogen, and approximately for the so-called Rydberg states.

So using E=h*v and Planck's constant. a simple factor of 1/h would return the frequency.
right?

Yes.

Is there an equation that models atomic spectra of all atoms?

As far as I know, no. We haven't derived the general expression for energy levels for all atoms.

 

[Xilus]

is the spectra the same for all isotopes?

 

[blue_leaf77]

is the spectra the same for all isotopes?

There is the so-called isotope shift which arise due to the fact that the nucleus is not completely at rest. It moves around by a very little amount which in turn disturbs the motion and hence wavefunction and energy levels of electrons. Different nuclear mass will have different effect on the wavefunction.

 

[Khashishi]

The formula for the isotope shift is quite simple. It's just a scaling by the reduced mass.
The energy is
$$E_M = \frac{M}{m_e+M} E_\infty \left(\frac{1}{n_1^2} - \frac{1}{n_2^2}\right)$$
where $m_e$ is the electron mass, $M$ is the nuclear mass, and $E_\infty \approx 13.605693$ eV

 

[gianeshwar]

I think quantum mechanics brings in probabilities into physics ,so due to no determinism we cannot describe a general result for multielectron atoms.

 

[Khashishi]

That's not the reason we don't have a general result. The reason is that it's just too complicated for a simple analytical formula.