Discussion Overview
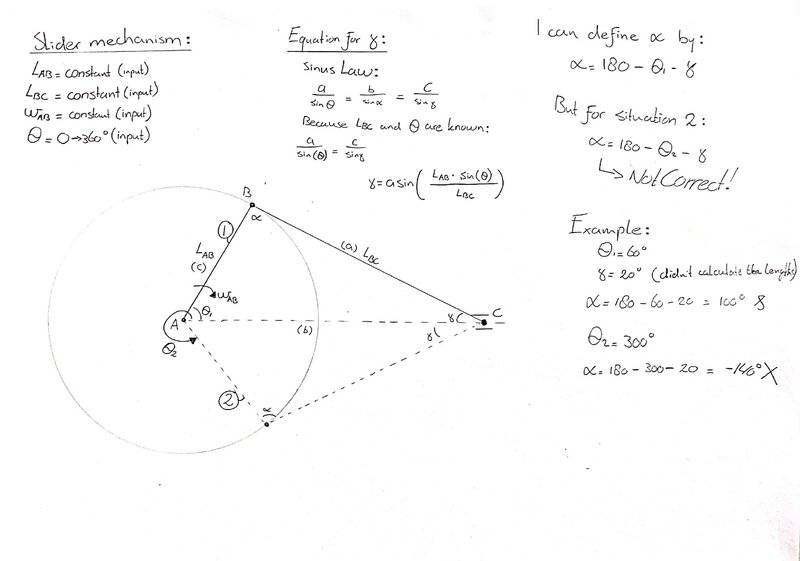
The discussion revolves around deriving an equation for the angular position (α) in a slider crank mechanism, given the lengths of the rods and an input angle (θ). Participants explore the complexities that arise when the mechanism's configuration passes 180 degrees, leading to challenges in formulating a consistent equation for all angle inputs.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant seeks a formula for α that accommodates angles from 0 to 360 degrees without introducing sign changes when θ exceeds 180 degrees.
- Another participant suggests establishing a systematic method for measuring angles to ensure consistency across definitions of α and γ.
- There are discussions about the definitions of angles ACB, ABC, and CAB in different configurations of the mechanism.
- Participants present equations involving trigonometric functions and the law of sines to relate the lengths of the rods and angles.
- Concerns are raised about the validity of certain equations, particularly regarding the square root terms and their implications for physical constraints.
- One participant mentions difficulties in determining the angle between velocities Vb and Vb' and how reference angles can lead to negative values.
- Another participant highlights that negative values under the square root indicate a design constraint, specifically when one rod length exceeds another, leading to potential binding in the mechanism.
Areas of Agreement / Disagreement
Participants express various viewpoints on the definitions and equations related to the mechanism, with no consensus reached on a single formula that resolves all issues. Disagreements persist regarding the treatment of angles and the implications of certain configurations.
Contextual Notes
Limitations include unresolved assumptions about angle definitions, dependencies on specific configurations, and the implications of negative values under square roots in the context of physical constraints.
Who May Find This Useful
Readers interested in mechanical engineering, kinematics, or those working on similar slider crank mechanisms may find the discussion relevant.