anon6912
- 21
- 3
I have a system with three inductors connected together at a common point.
The unconnected ends of each inductor is connected to an independent voltage source.
Basically I want to get three expressions for the dynamics of the currents with V1, V2 and V3 as inputs.
i.e. i need to eliminate the intermediary variable VT.
I want to write the state equations for the system in the following format (state space form):
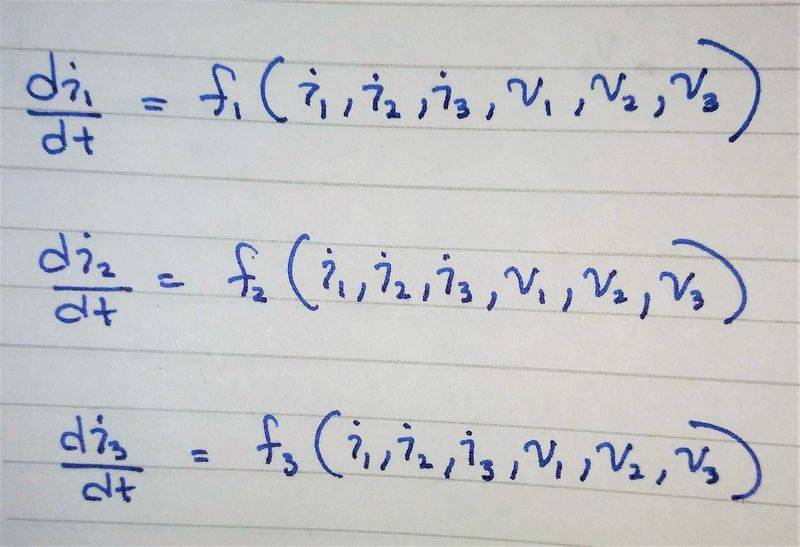
The system and, how far i got is below:
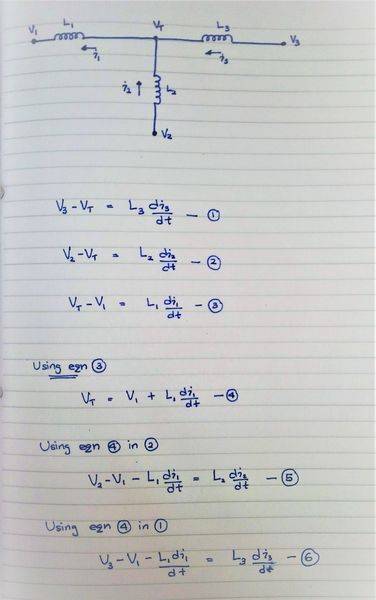
I don't know how to proceed from here.
Or is it impossible to get it into the format I want?
The unconnected ends of each inductor is connected to an independent voltage source.
Basically I want to get three expressions for the dynamics of the currents with V1, V2 and V3 as inputs.
i.e. i need to eliminate the intermediary variable VT.
I want to write the state equations for the system in the following format (state space form):
The system and, how far i got is below:
I don't know how to proceed from here.
Or is it impossible to get it into the format I want?


