Equations needed for force required to lift water Take 2

[Baxidur]

Hello

I posted something similar to this last week but maybe I was a touch vague as I didn't receive any good answers, So here some more details.

I'm looking for the equations required to calculate this and also any variations in the size of the cylinders/distance lifted

If I have 2 cylinders:-
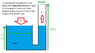
Cylinder A 10cm diamter, 10cm high
Cylinder B 1cm diamter, 20cm high
They are both at ground level and conected via a 1cm pipe at the base of the cylinders

A, How can I calculate the force required on cylinder A to lift the water in cylinder B a given distance, i.e 5 cm
B, How can I calculate the required on cylinder B to completely empty cylinder A into (and overflowing B at 20cm high)

Yours hopefully

Mark Nutley

 

[tiny-tim]

Welcome to PF!

Hello Mark! Welcome to PF!

Well, the work-energy equation solves just about anything …

can you apply it here? ​

 

[Baxidur]

Hi and thanks for the welcome tiny tim.

I have never heard of that equation, and my calculator doesn't have a 'work' or 'energy' button

But thanks for trying, guess I'll spend another day using google to try and figure it out myself and if that fails I can always buy all the materials to run the various experiments and try and build the equations myself, (working full time so it may take a while) I'll post them some time next year and you can check them against the originals to see if I got it right if that's ok?

Thanks again

Mark Nutley

 

[sk9]

HI!
Well it is strange that you are doing fluid and have not covered work energy. Anyways what is the approach you are familiar with or trying to think of.

Your question is not complete, see lifting water (to a distance)needs not only force but an amount of time on which it is applied.

You can find that just near equilibrium force by equating the pressures at same horizontal level or by Bernoullis equation(both are a form of work energy theorem by the way)

Hope that helps
Please reply if you have esome other approach I would love to learn a new one

 

[Baxidur]

Hi Sk9

Thanks for the imput, I'm a mechanic by trade with no formal education, learning physics on the fly because it interests me.
Sorry I never though about time, it doesn't have to be fast, hours is fine.

 

[tiny-tim]

Hi and thanks for the welcome tiny tim.

I have never heard of that equation, and my calculator doesn't have a 'work' or 'energy' button

But thanks for trying, guess I'll spend another day using google to try and figure it out myself and if that fails I can always buy all the materials to run the various experiments and try and build the equations myself, (working full time so it may take a while) I'll post them some time next year and you can check them against the originals to see if I got it right if that's ok?

Thanks again

Mark Nutley

yes, that's fine … i'll get my people to clear a gap in my schedule for an hour on 16th may 2013 so that i can look at it

in the meantime, work done is force times distance, and the work energy theorem says that work done = change in total mechanical energy (in this case, kinetic energy + potential energy)
​

 

[meldraft]

http://en.wikipedia.org/wiki/Bernoulli's_principle

You can basically apply the principle along the 2 cross sections you are interested in. Pressure is Force/Area, so you can figure out the force from that.

The other equation you will need is the conservation of mass:

\frac{d}{dt}mass_{cross section1}=\frac{d}{dt}mass_{cross section2}

\frac{d}{dt}mass=density*AreaOfCrossSection*Velocity

 

[sk9]

Hi Mark Nutley,
well if have lots of time then CONGRATULATIONS, you will be wasting least amount of energy,(when you speed some thing you waste energy in speeding things though you just want to go to your next position and then you waste energy in slowing it down at its final postion to stop) and you don't even need to apply Bernuolli equation you can just equate pressures at same heights in the same continuous liquid

use pascals[/PLAIN] law Hydraulic ramps are based on this principle.