PwnagePanda
- 3
- 0
Equivalent capacitance... A hard one!?
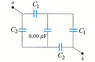
Calculate Equivalent capacitance between A and B:
[PLAIN]http://scsupport.org/moodle/file.php/13/Chapter26/imgch26q14.gif
EDIT: If you can't see the picture, see 3rd post for file attachment, sorry!
C1 = 3.55 µF
C2 = 1.90 µF
I know how to solve for equivalent capacitance with capacitors in series and parallel, but not both at the same time! Unless I'm seeing the problem wrong this is a complicated problem that I have never seen before! My mind is blown...
Any help at how to approach this would be greatly appreciated!
Homework Statement
Calculate Equivalent capacitance between A and B:
[PLAIN]http://scsupport.org/moodle/file.php/13/Chapter26/imgch26q14.gif
EDIT: If you can't see the picture, see 3rd post for file attachment, sorry!
Homework Equations
C1 = 3.55 µF
C2 = 1.90 µF
The Attempt at a Solution
I know how to solve for equivalent capacitance with capacitors in series and parallel, but not both at the same time! Unless I'm seeing the problem wrong this is a complicated problem that I have never seen before! My mind is blown...
Any help at how to approach this would be greatly appreciated!
Last edited by a moderator: