Equivalent Impedance: 1MicroF Cap, 1kOhm & 200mH Inductor

[jmartin]

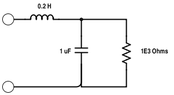
Question: A 1-microF capacitor and a 1-kOhm resistor are connected in parallel, and this parallel combination is connected in series with a 200-mH inductor. Find the equivalent impedance of the connection at w=1 krad/s.

Relevant Equations: Z=R for a resistor, Z=jwl for an inductor, and Z=1/(jwC) for a capacitor (w=omega)

I know to find equivalent impedance you use the above equations, but I am not sure how to proceed with this question. Any help would be appreciated.

 

[Ackbach]

So we have the following:

View attachment 4513

And you have reported $\omega=1E3$ rad/s. So what are the individual impedances?

 

[jmartin]

The impedances are 1000 ohms for the resistor, 200j for the inductor, and 1000/j for the capacitor.

 

[Ackbach]

The impedances are 1000 ohms for the resistor, 200j for the inductor, and 1000/j for the capacitor.

Excellent! I'd go ahead and write $1000/j=-1000j$, since $\dfrac{1}{j}=-j$.

So, now we have to consider how these elements combine. How are the components connected? And how do impedances combine in series? Parallel?

 

[jmartin]

The capacitor and resistor are connected in parallel, and this combination is in series with the inductor. Impedances are added normally in series and inversely in parallel.

 

[Ackbach]

The capacitor and resistor are connected in parallel, and this combination is in series with the inductor. Impedances are added normally in series and inversely in parallel.

Excellent! So your equivalent impedance is...

 

[jmartin]

I am getting 1000-487j as the answer. I'm not sure what I am doing wrong in my calculations.

 

[Ackbach]

Ok, so we should have
\begin{align*}Z_{\text{eq}}&=200j+(1000) \| (-1000j) \\
&=200j+\frac{(1000)(-1000j)}{1000-1000j} \\
&=200j+\frac{-1000j}{1-j} \\
&=200j+\frac{-1000j}{1-j} \cdot \frac{1+j}{1+j} \\
&=200j+\frac{-1000j+1000}{2} \\
&=200j+500-500j \\
&=500-300j.
\end{align*}
Can you see your error now?

 

[jmartin]

Yes I found where I made my mistake. Thank you so much for your help!

 

[Ackbach]

You're quite welcome! Any time!