Equivalent system (force+couple moment) of a loaded beam

[greg_rack]

Homework Statement

Replace the loading by an equivalent force and couple moment acting at point O(drawing attached below)

Relevant Equations

Torque=r x F (vectorial)

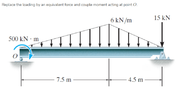
Hi guys,

I don't really know how to cope with this problem, maybe just because I can't properly understand the data.
In the figure we have a beam with its loading(plus a force of 15kN), a pivot O and support at the rightmost point.
I would say that in order to find the equivalent system, I must find the resultant force(by taking the integral of the wing load function over the beam lentgth) on the beam and its point of application, so that I can calculate the torque it produces and add it to the already present 500kNm(so I be able to move the force to point O).
The problem is I don't know how to interpret the function of the beam load. In the drawing it says 6kN/m, but in which way? Does it only apply until x=7.5m, or how would you interpret it?

 

[Chestermiller]

You have a distributed load that peaks at 6 kN/m at 7.5 m, and decreases linearly to zero at either side of the peak. Do you know how to deal with distributed loads?

 

[greg_rack]

You have a distributed load that peaks at 6 kN/m at 7.5 m, and decreases linearly to zero at either side of the peak. Do you know how to deal with distributed loads?

uhmm, so it means that from x=0 up to x=7.5m, my "load function" would be $f(x)=(6k\frac{N}{m})x$, before it starts decreasing linearly

 

[haruspex]

uhmm, so it means that from x=0 up to x=7.5m, my "load function" would be $f(x)=(6k\frac{N}{m})x$, before it starts decreasing linearly

If the load density is $f(x)=(6\frac{kN}{m})x$, what is its value at x=7.5m? You need that to be 6kN/m.

 

[Chestermiller]

uhmm, so it means that from x=0 up to x=7.5m, my "load function" would be $f(x)=(6k\frac{N}{m})x$, before it starts decreasing linearly

The load between x and x +dx in this region would be $6\times\frac{x}{7.5}dx$

 

[greg_rack]

The load between x and x +dx in this region would be $6\times\frac{x}{7.5}dx$

And why? Actually I don't think I can deal with distributed loads yet. I interpreted the problem in a different way... tomorrow I'll try to grasp more about this topic and let you know if the problem gets clearer!

 

[haruspex]

And why? Actually I don't think I can deal with distributed loads yet. I interpreted the problem in a different way... tomorrow I'll try to grasp more about this topic and let you know if the problem gets clearer!

View it as a graph of y against x. At x=0, y=0; at x=7.5(m), y=6(kN/m). What is the equation for y?

 

[greg_rack]

Alright, I made a few steps backwards and managed to get to an answer(even if probably not by taking the shortest path): I found the $w(x)$ function first from 0 to 7.5m, then from 7.5m to 12m and integrated it along the length of the beam to find the two resultant forces.
Finally I calculated the points on the beam's surface from where pass the lines of action(centroids of the two triangles) of the two forces, to get the two torques in order to find the equivalent couple moment

 

[haruspex]

Alright, I made a few steps backwards and managed to get to an answer(even if probably not by taking the shortest path): I found the $w(x)$ function first from 0 to 7.5m, then from 7.5m to 12m and integrated it along the length of the beam to find the two resultant forces.
Finally I calculated the points on the beam's surface from where pass the lines of action(centroids of the two triangles) of the two forces, to get the two torques in order to find the equivalent couple moment

Sounds ok. What answers did you get?

 

[greg_rack]

Sounds ok. What answers did you get

Hence I got a total moment and a total resultant force. In order to get to the equivalent system I shifted the force to point O and defined a couple moment equal to the resultant torque acting on the beam(two loadings+given moment+torque caused by the given force)