Understanding The Concept Of Moments

[tomtomtom1]

Homework Statement

- Turning Moment

- Bending Moment

- Moment of Force

Relevant Equations

- Turning Moment

- Bending Moment

- Moment of Force

Hello all;

I am trying to better understand the idea of Moments.

I know how to calculate moments i.e. Distance * Perpendicular Force.

My understanding was that moments were any push/pull force that creates a turning action about some point - that is what a moment is to me, I have shown this in the diagram below:-

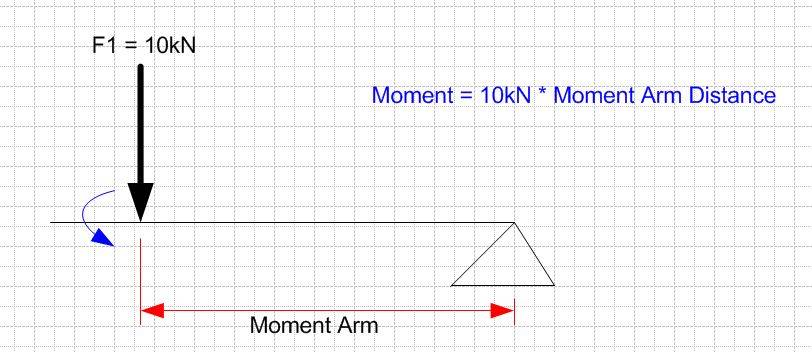However people have used the terms:-

- Turning Moment
- Bending Moment
- Moment of Force

It is these terms that are confusing me. I think Turning Moment and Moment of Force are the same thing & these terms satisfy my definition of what a Moment is (please say I'm right).

But the term Bending Moment has been used with the following diagram:-

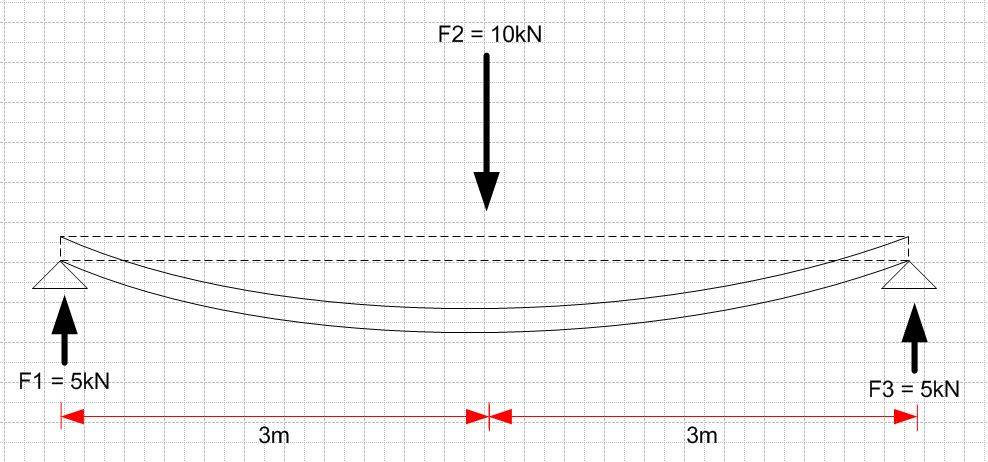
In this diagram I feel that the term Bending Moment means something different and its confuses me. I thought that Bending Moment in this case meant calculating how much the beams bend from its original position but I have since been told that this is incorrect.

I can see how a turning action can be cause because the F2 (10kN) force acting downwards taken about F1 would introduce a clockwise turning action, so I would get Moment Taken About F1 = 3 * 10kN = 30kNm.

But what does 30kNm moment taken about F1 actually mean?

Is the 30kNm acting at position F1 or acting at position F2?

Is 30kNm another force, is it a force that internal to the beam ?

I really was hoping someone could explain.

Thank you.

 

[haruspex]

But what does 30kNm moment taken about F1 actually mean?

Is the 30kNm acting at position F1 or acting at position F2?

It is the same as turning moment, both being torque. But typically we discuss bending moment in a static context, so nothing actually turns.
The 10kN force acts at F2, but the moment of 30kNm is about F1. This is countered by the anticlockwise moment of 30kNm from the 5kN force at F3.

 

[tomtomtom1]

Thank you for your reply.

I just realized that there is a difference between Moment and Bending Moment, Moment is External and describes rotation and Bending Moment is an internal reaction to bending.

Anyway going back what I say about the Moment taken about F1 being 30kNm - would it be correct in saying that the rotation at F1 can be quantified as being 30kNm - would this be a correct statement?

Thank you.

 

[haruspex]

Bending Moment is an internal reaction to bending.

You are probably right, technically, though in statics it makes little difference whether you think of it as the reactive moment (on a given side of the point) or the total applied moment from that side, the two being equal but opposite. https://en.m.wikipedia.org/wiki/Bending_moment defines it as the reaction, but the rest of the article freely switches between the two views.
In a kinetic situation, the two will not be equal and opposite.

the rotation at F1 can be quantified as being 30kNm

Not sure what you mean. There is no rotation. There is no bending moment there either since the sum of the applied moments to one side of it (left or right) is zero.

 

[haruspex]

Thinking about it some more, if we take bending moment as the reaction then the difference is analogous to that between force and tension (or compression). Tension is not a force , exactly; the tension at a point is a pair if equal and opposite forces acting one each side of the point. Likewise, the bending moment (reaction) at a point is a pair of equal and opposite moments acting one each side of the point.

 

[tomtomtom1]

Haruspex

Thank you for your reply.

I have to be honest, I'm still struggling a little.

Using my previous example, shown below:-

I have calculated the Moment (which is an external force that describes rotation) about F1 (the dotted line is the neutral axis).

By taking all the moments/rotations from F1 results in a value of 0 means that this beam will not rotate.

I hope this is correct so far.

I know that the 10kN load will bend the beam so that the top of the beam will be in compression and the bottom of the beam will be in Tension

If I was to cut the beam 1.5m away from F1 to determine the Bending Moment which I know are the internal reactions induced by the external load to resist bending then I would get the following:-

The top of the beam is in compression which results in an internal reaction which is opposite to the compression (shown in green), these opposite reactions are largest at the top and getting smaller as I approach the neutral axis.

Once I past the neutral axis towards the bottom on the beam, the beam is in tension and a reaction is created in the opposite direction of the tension forces (shown in red), these forces get larger as I move further away from the neutral axis.

If I now calculate the Bending Moment at B1 I get a value of 7.5kNm but what I don't understand is that to calculate my bending moment at B1 is identical to calculating the external moment which is a rotation - Why are they the same calculation.

Also what does 7.5kNm mean? does it mean the amount of opposing forces between tension & compression 1.5m away??

Or are Moments and Bending Moments both calculating/determining Rotation and I have just lost my way in my thinking?

Your thoughts?

Thank you.

 

[haruspex]

which is an external force that describes rotation

As I wrote, a moment is not a rotation. It is the tendency of the force to induce a rotation. Rotation will only occur if the moments are unbalanced.

what does 7.5kNm mean?

Consider a simpler situation: tightening a nut with a wrench. A force of 5kN exerted normally at the end of a wrench length 1.5m will have exactly the same effect at the nut as a force of 1.5kN with a wrench length 5m. It is the product of the force and distance that matters.

to calculate my bending moment at B1 is identical to calculating the external moment which is a rotation

As I wrote, there is a subtle difference between bending moment, i.e. the internal reaction, and an applied moment. The bending moment is really a pair of equal and opposite moments.
Suppose a moment M_A is applied at one end of a beam and a moment M_B is applied at the other end.
If the two applied moments are equal and opposite then the system is static. Now pick some point C along the beam. The section AC does not rotate, so the reaction moment at C exerted on AC is -M_A. Similarly, the reaction moment exerted on CB is -M_B=+M_A. This pair of equal and opposite reaction moments is the bending moment at C.
Now consider an unbalanced case, M_A+M_B=M≠0. If the moment of inertia of the whole beam is I then there will be an angular acceleration α, where M=Iα. So AC and CB each undergo that angular acceleration. If AC has moment of inertia I_A then the net moment on that must be I_Aα, and we can deduce that the reaction moment at C on AC is I_Aα-M_A. The same analysis for CB will produce an equal and opposite reaction moment.

What you wrote about tension and compression is true, but I don't think it is necessary or helpful to think in those terms.