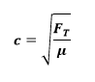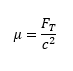Error calculation for µ in standing wave experiment

[rasalzari]

Homework Statement

I experimented with standing waves on an oscillating string, and I was asked to calculate the absolute error of µ (linear mass per unit length). I don't know how to calculate it, so please help me.
I loaded 100g, 200g and 300g on the string. Below are tabulated data of the experiment.

Homework Equations

I know the basics of uncertainties, but in here it's kinda complicated as I don't know how to calculate the tension or speed error. I know this formula:

where c= speed, FT= tension and µ = linear mass per unit length

making µ the subject:

The Attempt at a Solution

[/B]
So the calculated tension for the 3 sets of masses are:
100g = 9.81*0.1=0.981
200g= 9.81*0.2=1.962
300g= 9.81*0.3=2.943

Speed:
100g= 39 m/s
200g= 54 m/s
300g= 72 m/s

µ values:
100g -> 0.981/39^2 = 644.9*10^-6 kg/m
200g -> 1.962/54^2 = 672*10^-6 kg/m
300g -> 567.7*10^-6 kg/m

Do i like average the tension and speed values and subtract the max and min number

So if i do that then:

average of tension = 1.962
2.943-0.981=1.962 <- this is the uncertainty?

average of c^2:

• averaging -> 39+54+72/3 =55
• squaring -> 55^2 = 3025

72-39= 33
72^2-39^2=3663

This seems very wrong i don't really know what I'm doing.

 

[kuruman]

You absolutely do not average the tensions or the speeds. You average only quantities that are supposed to be the same in order to reduce the uncertainty in the measurements. Since the speed depends on the load, you can average the speeds that you get with the same load for different harmonics. That would make sense. It makes no sense to average speeds for different loads because you know they are different and you know why they are different so what good would it do to you if you average them?

You say you understand the basics of error propagation. You have quoted the uncertainties in f, L and λ. How about the uncertainty in F_T? Can you estimate that? If so, find an expression for μ in terms of the experimentally measured quantities and do error propagation analysis. Also note that you have 15 measurements you can use to calculate 15 values of μ separately. Find what these are and see if they are consistent with the error propagation anlysis.