Remixex
- 57
- 4
- Homework Statement
- Suppose that seismic observation shows that P wave arrives 14 min later at 110 degrees epicentral distance for shallow earthquakes. Between 110 and 140 degrees is the P wave shadow zone. Assuming the Earth can be simplified as two homogeneous parts, the mantle and the core, derive and plot the P travel-time curve T(∆). Estimate P velocities of the mantle and core and the size of the core from the observation. Assume the radius of the Earth is Rt = 6371 km.
- Relevant Equations
- Snell's law, trigonometry relationships, arc length of the Earth.
Hello, this is a repost from a much less-clear question I posted before (link to question: https://www.physicsforums.com/threa...s-inside-an-ideal-earth.1011998/#post-6596165).
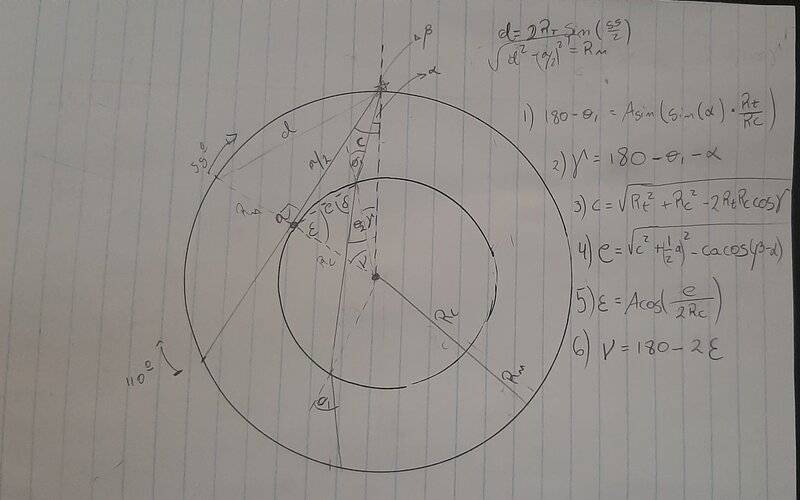
It's kind of a loaded question, however it can be expressed as triangles within a circle or a sphere, as shown in the image. Given the available information (that the P wave takes 14 minutes to travel 110 degrees, or 12232 kilometers of arc length) I obtained the linear distance the P-wave travels through in the mantle, I named it ##a## and it is about 10438 kilometers. With this we can get the velocity through the idealized mantle, at about 12.43 kilometers per second. (##\frac{a}{14*60} km/s ##)
Then, using half of this distance ##a/2##, knowing it is tangent to the core and that it can form a right triangle with a distance ##d## that goes from the source to 55 degrees of epicentral distance and the distance from the surface of the core to the surface of the mantle, named ##R_m##. ##d=2*R_t*sin(55/2)## and then we can obtain ##R_m=\sqrt{d^2 - 0.25*a^2}## which is about 2717 kilometers, therefore the core radius is 3654 kilometers.
We can also do another right triangle, composed of the radius of the Earth, the radius of the core, and the distance ##a/2##. With this we can get the take-off angle ##\beta = Acos(((a/2)^2 + R_t^2 - R_c^2)/(a*R_t))##, which is 35 degrees.
Now it gets a little hairy, to get the velocity at the core we must apply Snell's law. For this I assumed there is a second ray that enters the core with a take off angle ##\alpha##, which is known, an incident angle ##\theta_1## and refracts with angle ##\theta_2## at the surface of the core.
The triangle composed by ##R_t##, ##R_c## and the distance traveled by this new ray ##c## can be completely obtained through law of cosines, given that we also know the take-off angle ##\alpha##. Using this triangle I obtained the incident angle ##\theta_1## (equations in the image 1, 2 and 3)
This is where I get stuck. Equations 4 through 6 are my attempts at trying to get the refracted angle ##\theta_2##, which is key to obtain the velocity through the core via Snell's law. But I could only reach a bigger angle ##\epsilon=\delta + \theta_2##.
I feel like I am missing something, a triangle I have not drawn to obtain ##\theta_2##.
Thank you for reading. Any direction is greatly appreciated.
It's kind of a loaded question, however it can be expressed as triangles within a circle or a sphere, as shown in the image. Given the available information (that the P wave takes 14 minutes to travel 110 degrees, or 12232 kilometers of arc length) I obtained the linear distance the P-wave travels through in the mantle, I named it ##a## and it is about 10438 kilometers. With this we can get the velocity through the idealized mantle, at about 12.43 kilometers per second. (##\frac{a}{14*60} km/s ##)
Then, using half of this distance ##a/2##, knowing it is tangent to the core and that it can form a right triangle with a distance ##d## that goes from the source to 55 degrees of epicentral distance and the distance from the surface of the core to the surface of the mantle, named ##R_m##. ##d=2*R_t*sin(55/2)## and then we can obtain ##R_m=\sqrt{d^2 - 0.25*a^2}## which is about 2717 kilometers, therefore the core radius is 3654 kilometers.
We can also do another right triangle, composed of the radius of the Earth, the radius of the core, and the distance ##a/2##. With this we can get the take-off angle ##\beta = Acos(((a/2)^2 + R_t^2 - R_c^2)/(a*R_t))##, which is 35 degrees.
Now it gets a little hairy, to get the velocity at the core we must apply Snell's law. For this I assumed there is a second ray that enters the core with a take off angle ##\alpha##, which is known, an incident angle ##\theta_1## and refracts with angle ##\theta_2## at the surface of the core.
The triangle composed by ##R_t##, ##R_c## and the distance traveled by this new ray ##c## can be completely obtained through law of cosines, given that we also know the take-off angle ##\alpha##. Using this triangle I obtained the incident angle ##\theta_1## (equations in the image 1, 2 and 3)
This is where I get stuck. Equations 4 through 6 are my attempts at trying to get the refracted angle ##\theta_2##, which is key to obtain the velocity through the core via Snell's law. But I could only reach a bigger angle ##\epsilon=\delta + \theta_2##.
I feel like I am missing something, a triangle I have not drawn to obtain ##\theta_2##.
Thank you for reading. Any direction is greatly appreciated.
