Euler-Lagrange equations and the principle of least action

[JD_PM]

Summary:: I am missing something in my integration by parts

Consider the infinitesimal variation of the fields $\phi_a (x)$

$$\phi_a \rightarrow \phi_a + \delta \phi_a$$

The infinitesimal variation vanishes at the boundary of the region considered (ie. $\delta \phi (x) = 0$ at the boundary).

The definition of an action is

$$S = \int d^4 x \mathcal{L}(\phi, \partial_{\mu} \phi)$$

The infinitesimal variation of it is

$$\delta S = \int d^4 x \Big( \frac{\partial \mathcal{L}}{\partial \phi_a} \delta \phi_a + \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta (\partial_{\mu} \phi_a)\Big)$$

Where I have used

$$\delta \phi_a = \frac{\partial \phi_a}{\partial x^{\mu}} \delta x^{\mu} = \partial_{\mu} \phi_a \delta x^{\mu}$$

Well I know that I have to integrate by parts here. What I have done is

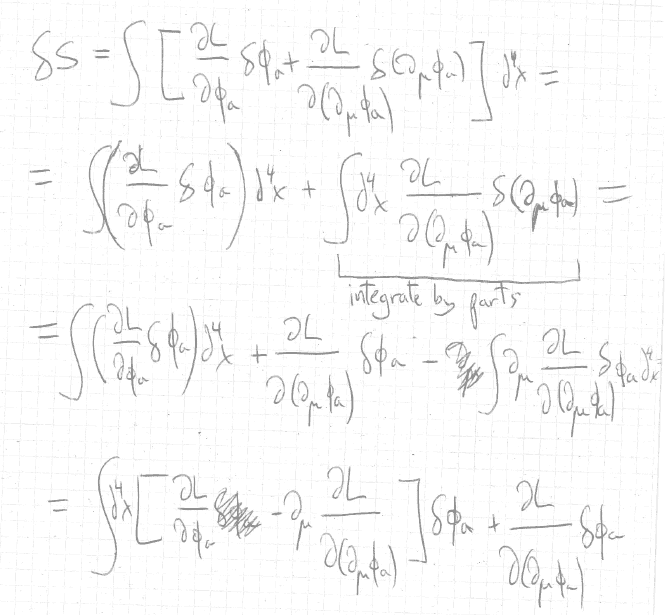
But this is not the same that what Tong got

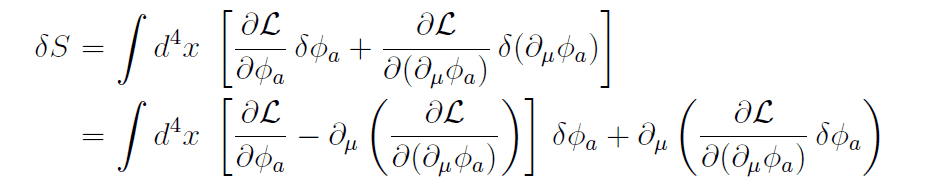
Note that I am missing $\partial_{\mu}$ in front of the second term. But I do not see why there should be one.

Thanks.

Reference: Tong's QFT Lecture notes, classical field theory, page 8.

 

[George Jones]

Well I know that I have to integrate by parts here. What I have done is


View attachment 258348

But this is not the same that what Tong got

View attachment 258349

Note that I am missing $\partial_{\mu}$ in front of the second term. But I do not see why there should be one.

Thanks.

Reference: Tong's QFT Lecture notes, classical field theory, page 8.

Tong has a typo. In the second line of equation (1.5), the right square should be at the end of the line.

 

[JD_PM]

Hi George Jones, thanks for the reply.

I’ve been thinking this may not be the best forum to ask this question, as my issue it’s more about Math (integration by parts).

I will report it.

 

[JD_PM]

Alright, after some thought I understood that the term $\int \partial_{\mu} \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a\Big) d^4 x$ does vanish because it is a total derivative and $- \int \partial_{\mu} \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a\Big) d^4 x$ does not vanish because it is (I think) a time derivative.

My point is: isn't notation confusing to you? I mean, if we are talking about different derivatives, why are we using the same notation $\partial_{\mu}$?

 

[Gaussian97]

No, is easier than that, you must start by noticing that $\delta (\partial_\mu \phi_a)=\partial_\mu \delta\phi_a$ (actually it depends on how do you define things, but if you want all the details you must go to a more rigorous book). Then use the product rule $\partial_\mu (ab) =a \partial_\mu b+b\partial_\mu a$ and you will get equation 1.5

Until here you have not dropped anything, and there's no typo in Tong's notes (although this notation of putting the differential at the beginning confuses a little bit). It's only now, that you use divergence theorem to perform the integral
$$\int \partial_\mu\left(\frac{\partial \mathcal{L}}{\partial (\partial_\mu\phi_a)}\delta\phi_a\right)d^4x$$
And only now you can apply the boundary conditions to get Euler-Lagrange equations.

 

[JD_PM]

Then use the product rule $\partial_\mu (ab) =a \partial_\mu b+b\partial_\mu a$ and you will get equation 1.5

Mmm I am afraid I do not agree. It is about partial differentiation, not the product rule.

 

[Gaussian97]

I don't get what you say.
If you mean that you don't need to use $\partial_\mu (ab) = a\partial_\mu b + b\partial_\mu a$ because the problem is not about the 'product rule' then I'm afraid to say that any problem can involve any equation.

If you mean that $\partial_\mu (ab) = a\partial_\mu b + b\partial_\mu a$ is called 'partial differentiation' instead of 'product rule' then ok, you can call it whatever you want.

By what I see in your attempt, you are more used to do the two steps I said (product rule + divergence theorem) in a single step that you call 'integration by parts'.
Actually there is where you have your error (in the 4th equal sign), I suggest you to try to do it with the two steps I give you.

 

[JD_PM]

I don't get what you say.

The point is solving the integral $\int \partial_{\mu} \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a\Big) d^4 x$ by integration by parts method (https://en.wikipedia.org/wiki/Integration_by_parts)

That explains why we pick a minus sign in one of the terms of the final result.

You seem to suggest applying the product rule we all know. However, you do not pick the minus sign doing so.

It turns out that partial integration is also known as 'a version of the product rule'. The misunderstanding seems to be coming from that fact.

 

[nrqed]

Alright, after some thought I understood that the term $\int \partial_{\mu} \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a\Big) d^4 x$ does vanish because it is a total derivative and $- \int \partial_{\mu} \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a\Big) d^4 x$ does not vanish because it is (I think) a time derivative.

My point is: isn't notation confusing to you? I mean, if we are talking about different derivatives, why are we using the same notation $\partial_{\mu}$?

As George pointed out, there is a typo in Tong's notes.
I don't understand what you wrote here as you wrote exactly the same expression twice (apart from the overall sign). Both of them are zero (for fields obeying as usual that $\delta \phi_a=0$ at infinity).

 

[Gaussian97]

The point is solving the integral $\int \partial_{\mu} \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a\Big) d^4 x$ by integration by parts method (https://en.wikipedia.org/wiki/Integration_by_parts)

That explains why we pick a minus sign in one of the terms of the final result.

You seem to suggest applying the product rule we all know. However, you do not pick the minus sign doing so.

It turns out that partial integration is also known as 'a version of the product rule'. The misunderstanding seems to be coming from that fact.

As I said, integration by parts IS a consequence of the product rule and divergence theorem, don't matter what you call it, and as I said, your error is in the 4th equality and is because you don't apply correctly the "integration by parts" rule, and is an error that wouldn't be there if you apply product rule + divergence theorem separately.

As George pointed out, there is a typo in Tong's notes.

I don't see any typo, at least in equation 1.5, what typo are you thinking about? Because in George post I understand he means that 1.5 should read as
$$\int \left[\frac{\partial \mathcal{L}}{\partial \phi_a} - \partial_\mu \left(\frac{\partial \mathcal{L}}{\partial (\partial_\mu \phi_a)}\right)\delta \phi_a + \partial_\mu \left(\frac{\partial \mathcal{L}}{\partial \partial_\mu \phi_a}\delta\phi_a\right)\right]d^4 x$$
And this of course is wrong.

 

[George Jones]

I don't see any typo, at least in equation 1.5, what typo are you thinking about? Because in George post I understand he means that 1.5 should read as
$$\int \left[\frac{\partial \mathcal{L}}{\partial \phi_a} - \partial_\mu \left(\frac{\partial \mathcal{L}}{\partial (\partial_\mu \phi_a)}\right)\delta \phi_a + \partial_\mu \left(\frac{\partial \mathcal{L}}{\partial \partial_\mu \phi_a}\delta\phi_a\right)\right]d^4 x$$
And this of course is wrong.

Oops (for me). I still maintain that there is a typo in Tong's (1.5), but, unfortunately, my "correction" above doesn't fix the typo. You implicitly corrected Tong's typo when you wrote

It's only now, that you use divergence theorem to perform the integral
$$\int \partial_\mu\left(\frac{\partial \mathcal{L}}{\partial (\partial_\mu\phi_a)}\delta\phi_a\right)d^4x$$

In (1.5), Tong writes

$$\int d^4 x \left[\frac{\partial \mathcal{L}}{\partial \phi_a} - \partial_\mu \left(\frac{\partial \mathcal{L}}{\partial (\partial_\mu \phi_a)}\right) \right]\delta \phi_a + \partial_\mu \left(\frac{\partial \mathcal{L}}{\partial \partial_\mu \phi_a}\delta\phi_a\right) .$$

This should be written as

$$\int d^4 x \left\{ \left[\frac{\partial \mathcal{L}}{\partial \phi_a} - \partial_\mu \left(\frac{\partial \mathcal{L}}{\partial (\partial_\mu \phi_a)}\right) \right]\delta \phi_a + \partial_\mu \left(\frac{\partial \mathcal{L}}{\partial \partial_\mu \phi_a}\delta\phi_a\right) \right\} .$$

 

[Gaussian97]

Ah, ok I see, I don't think it is a typo, I think the writer supposes that anyone must understand that the integral goes all the way until the end (for this reason I think that putting the $d^4 x$ at the end of the integral is much better).

So yes, even if we call it typo or not, of course, we need to understand that everything is inside the integral.

 

[JD_PM]

OK so let us go step by step

1) Apply the product rule (i.e. $\partial_\mu (ab) = a\partial_\mu b + b\partial_\mu a$) to $\int d^4 x \partial_{\mu} \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a \Big)$


$$\int d^4 x \partial_{\mu} \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a \Big) = \int d^4 x \Big( \partial_{\mu} \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a \Big) + \int d^4 x \Big( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta (\partial_{\mu} \phi_a) \Big)$$

But note I do not pick a minus sign. That was my point.

 

[Gaussian97]

Ok, now, remember that your starting point is the integral
$$\int \frac{\partial \mathcal{L}}{\partial \phi_a} \delta \phi_a d^4x + \int\frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta (\partial_{\mu} \phi_a) d^4 x$$
Look that the second term in your right hand side is exactly one of the integrals you are looking for, now you can isolate this integral to get
$$\int \frac{\partial \mathcal{L}}{\partial \phi_a} \delta \phi_a d^4x +\int \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a \right)d^4 x - \int \partial_{\mu} \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a d^4 x$$
(Note how the $-$ sign appears naturally), until here, it's very similar to what you have, but in your attempt now you do
$$\int \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a \right)d^4 x = \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a$$ this is your mistake (that was a little hidden because you did all this steps at once by applying "integration by parts"). Now, forget about this last equation that is not correct, and apply the divergence theorem to the integral
$$\int \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a \right)d^4 x$$

NOTE: I put all the $d^4x$ at the end of the integrals to avoid any misconception like the ones we had in the discussion with George, please read that posts because they are important if you understand the notation as George and nrqed do, then there is a typo in Tong notes, and you must write 1.5 as #11.

 

[JD_PM]

Ahhh thanks Gaussian97, I get it now!

But what is the difference between $\int \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a \right)d^4 x$ and $- \int \partial_{\mu} \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a d^4 x$?

I understand the math to get those two terms but to me they look the same and I would naively think that they cancel each other out. Why am I wrong?

 

[Gaussian97]

Ahhh thanks Gaussian97, I get it now!

But what is the difference between $\int \partial_{\mu} \left( \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a \right)d^4 x$ and $- \int \partial_{\mu} \frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a d^4 x$?

I understand the math to get those two terms but to me they look the same and I would naively think that they cancel each other out. Why am I wrong?

No, be careful, maybe I'm confusing you with my notation (in general I try to put as few parentheses as I can and sometimes it confuses people), these two terms are different, the second one must be understood as
$$\int \partial_{\mu} \left(\frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)}\right) \delta \phi_a d^4 x$$
notice the difference in what is inside the parenthesis (and therefore, what is inside the derivative), in the first case, you are differentiating the product $\frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)} \delta \phi_a$ i.e. you are looking at what is the variation of this product, while in the second case, you are differentiating only the term $\frac{\partial \mathcal{L}}{\partial(\partial_{\mu} \phi_a)}$, and then multiplying this "variation" with the function $\delta \phi_a$, the result is different (although you can relate them using the product rule).