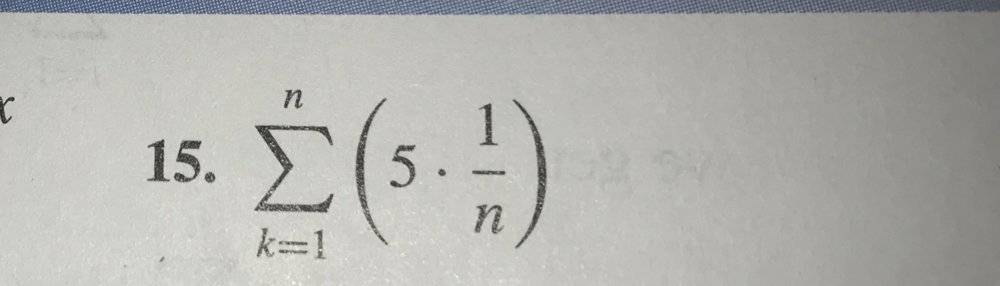The discussion centers around evaluating a sum where the answer is claimed to be 5, but confusion arises regarding the interpretation of the index and the summation process. Participants debate whether the sum should be evaluated over n or k, with some suggesting that a common arithmetic series table could clarify the solution. It is emphasized that if the index stops at one, the answer could misleadingly appear as 5, but this does not hold for larger values of n. Ultimately, the correct understanding is that the sum involves adding a constant term, leading to the conclusion that the answer remains 5 for any value of n. The conversation highlights the importance of carefully reading the problem to avoid misinterpretation.