- #1
elimenohpee
- 67
- 0
Homework Statement
Evaluate the integral:
Homework Equations
To integrate this, should one use a dummy variable to get the delta function only of t, then integrate, then substitute back in after integration?
elimenohpee said:Homework Statement
Evaluate the integral:
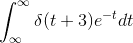
Homework Equations
To integrate this, should one use a dummy variable to get the delta function only of t, then integrate,
then substitute back in after integration?
The delta function, also known as the Dirac delta function, is a mathematical function that is defined as 0 for all values except at the origin, where it is infinitely large. It is used in integrals because it acts as a spike that concentrates the integral at a single point, making it easier to evaluate.
To evaluate the integral of a delta function, you need to determine the limits of integration and then use the properties of the delta function to simplify the integral. This usually involves rewriting the integral in terms of the delta function's argument and using the sifting property to eliminate other terms.
No, the delta function is only defined at a single point, so it cannot be integrated over a finite interval. However, you can use the properties of the delta function to evaluate an integral over a finite interval by dividing the interval into smaller intervals and integrating over each one.
The unit step function, also known as the Heaviside function, is defined as 0 for negative values and 1 for positive values. It is often used in conjunction with the delta function because its derivative is equal to the delta function. This means that the integral of the delta function can be expressed as the difference between the unit step function evaluated at the upper and lower limits of integration.
Yes, the delta function has many practical applications in fields such as engineering, physics, and signal processing. It is used to model impulsive forces, point sources, and impulse responses in systems. It is also used in the theory of distributions, which has applications in fields such as control theory and partial differential equations.