Exact electrostatic potential of a pure dipole using multipole expansion

[Ahmed1029]

TL;DR

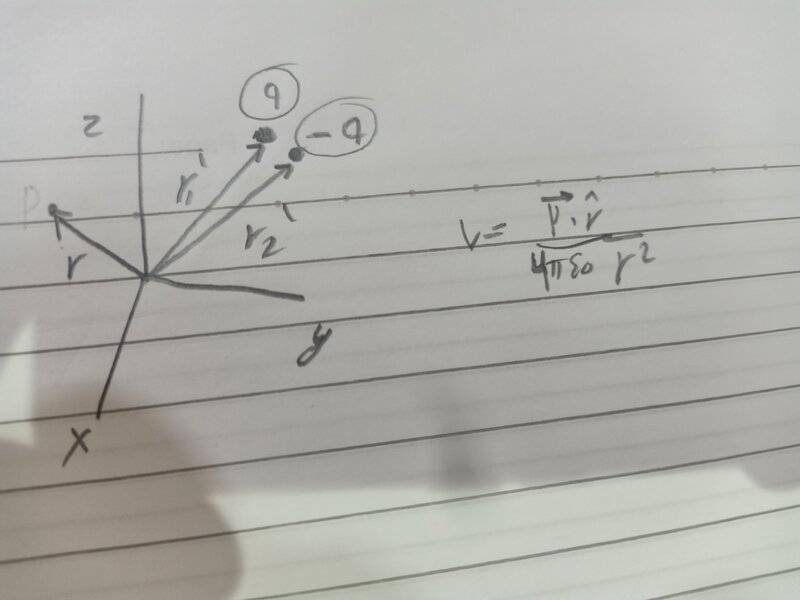
I'm confused when reading Griffiths electrodynamics as he says the mutlipole expansion of a pure dopole is exactly the dipole term everywhere in space, but I'm not sure if this is just true when the point dipole is at the origin of coordinatea or it could be anywhere.

If I have a physical dipole with dipole moment p. Now, this formula for potential (V) is a good approximation when r is much larger than both r1 and r2 in the picture below. It's however said that for a pure dipole for which the separation between charges goes to zero and q goes to infinity, the dipole potential given by V is exact, and here comes my problem : Is it only exact when r is larger than both r1 and r2? or can I find the potential for all points in space except the location of the point dipole? Is it exact for all points in space only when the location of the dipole is at the origin?I'll be glad if someone tries to help!

 

[kuruman]

Welcome to PF @Ahmed1029.

The dipole approximation is valid when $r>>|\vec r_2-\vec r_1|.$

 

[Ahmed1029]

Welcome to PF @Ahmed1029.

The dipole approximation is valid when $r>>|\vec r_2-\vec r_1|.$

Thanks you! I'm however still confused since there is no apparent restriction on r1 and r2, so they can themselves be very far. So my question is, when those two tiny chunks of charge are squeezed together at one point and I want to calculate the potential in space, does this one point have to be the origin for this formula to be exactly true and not just an approximation? Or it could be anywhere?

 

[Meir Achuz]

Point dipoles, like point charges, arise from Quantum excitations and their potential is exact, just like that of a point charge.

 

[kuruman]

Thanks you! I'm however still confused since there is no apparent restriction on r1 and r2, so they can themselves be very far. So my question is, when those two tiny chunks of charge are squeezed together at one point and I want to calculate the potential in space, does this one point have to be the origin for this formula to be exactly true and not just an approximation? Or it could be anywhere?

Yes, there is no restrictions to $\vec r_1$ and $\vec r_2$, but once you choose them, the distance between them, $d=| \vec r_1-\vec r_2|$, is fixed. Now imagine a sphere of diameter $d$. The dipole approximation is valid at points $r$ from the center of the sphere such that $r>>d$. The dipole potential is $V=\dfrac{k\vec p\cdot \vec r}{r^2}$ where the dipole is assumed to be at the origin. If you want the origin to be somewhere else such that the dipole is at $\vec r_d$ relative to it, the dipole potential must be written as $V=\dfrac{k~\vec p\cdot (\vec r-\vec r_d)}{|\vec r-\vec r_d|^2}$. In either case the distance between the charges must be much much smaller than the distance from either charge to the point of interest for the dipole approximation to be valid.

 

[Ahmed1029]

Oh cool! Just to make sure, when the origin is away from the dipole and I want to calculate the dipole potential using only the position vector r, not (r-rd), I need to include the other multipole terms and not just the dipole term in case of a pure dipole right?

 

[robphy]

In my 4th edition of Griffiths, the following passage may help

3.4.3 Origin of Coordinates in Multipole Expansions

I mentioned earlier that a point charge at the origin constitutes a "pure" monopole.
If it is not at the origin, it's no longer a pure monopole.
...
So moving the origin (or, what amounts to the same thing, moving the charge)
can radically alter a multipole expansion. The monopole moment Q does not
change, since the total charge is obviously independent of the coordinate system.
...
Ordinarily, the dipole moment does change when you shift the origin, but there is an important exception:
If the total charge is zero, then the dipole moment is independent of the choice of origin.
...