Expectation of Covariance Estimate

[brojesus111]

So I'm trying to take the expectation of the covariance estimate.

I'm stuck at this point. I know I have to separate the instances where i=j for the terms of the form E[XiYj], but I'm not quite sure how to in this instance.

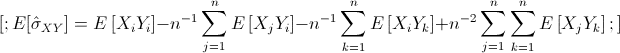
The answer at the end should be biased, and I'm trying to find a way to make it unbiased. But first tings first, I have to simplify the above.

 

[brojesus111]

Is this the next step? What's after that if so?

 

[chiro]

Hey brojesus111 and welcome to the forums.

I think you will have to incorporate the mean terms by putting something like + X_bar - X_bar.

Also given your expression, another that comes to find is try and complete the square in the way of getting E[(X-X_bar)(Y-Y_bar)] by matching this expression with the one you have been given.

The difference between the two will give the bias.