Explanation of the 'chain fountain': some doubts

[Brinx]

Apologies if this has been discussed in other threads already. I did a quick search on 'chain fountain' and got no hits.

If you coil a length of chain into a container and let it slip out over the lip under its own weight, it will start to form an arc through the air, without touching the lip of the container. See this youtube movie wherein this phenomenon is demonstrated and discussed:



I am having trouble believing the explanation that is put forward in that clip. Reaction forces from the 'table' (or in this case the surface of rest of the chain filling the container) do not perform any work and cannot cause the chain links to push one another upward into an arc shape.

I lean towards the explanation (not quite sure yet) that it is an inertial effect: as the chain gets dragged out of the container by the part that is slipping over the lip, it accelerates as more and more mass is falling down (and accelerating) on the other side. As it needs to change directions quite rapidly as it clears the lip (from upwards to downwards, with a small turning radius), the rotational inertia of the links causes them to whip out their rear end (the links have finite lengths) and pull the following link up a bit. The next link does the same, and the flow of links reaches an equilibrium height above the lip of the container.

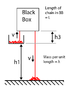
I suppose I should make it more clear by providing a diagram of the situation. In any case, I would welcome some discussion on this interesting phenomenon. I have already ordered a chain online to experiment myself. :)

 

[Andy Resnick]

Interesting- thanks for the link, I'll check it out shortly. Our science center has something similar, a 'lariat chain':
http://www.normantuck.com/catalogPages/lariat.html
that also behaves unexpectedly.

 

[dauto]

I think the point is that the table force on the rectangular bids does indeed perform work because the table is still in contact with one end while the other end (and center of mass of the bid) is already moving upward.

 

[John Biggins]

Hi. I'm one of the authors of the paper. The point you raise is a good one. The extra pushing force from the table is indeed a reaction force and, while it does impart momentum, it does not do any work. The point is that if you pick up a chain by pulling on it, only half the work done in the pulling ends up in the translational kinetic energy of the chain. This is a very general result (provided there is no anomalous push) but where the other half ends up depends on your model for the chain. For a chain of freely jointed rigid rods it ends up in rotational energy of the rods - each rod is picked up by a force at its end, so it starts both moving in the pull direction and rotating and ends up with equal amounts of rotational and translational kinetic energy. The anomalous force is a reaction force, so it does no work, but it changes some of this rotational energy into translational energy, so the chain leaves the pot faster and rotating less than it would have done.

 

[A.T.]

Interesting Problem.

the rotational inertia of the links causes them to whip out their rear end (the links have finite lengths) and pull the following link up a bit. The next link does the same, and the flow of links reaches an equilibrium height above the lip of the container.

but it changes some of this rotational energy into translational energy, so the chain leaves the pot faster and rotating less than it would have done.

So if Brinx is right, the rotation induced by the pull helps to form the fountain, due to angular momentum of individual links, which prevents them from going around the bend the shortest way.

If John is right, it's the reduction of that rotation by the ground reaction, that helps to form the fountain, by increasing the initial vertical linear momentum.

 

[DrClaude]

In the original Mould experiment, isn't the fact that there is a maximum angle between three consecutive beads vital? In that case, wouldn't the extra force come from the chain inself, through resistance to bending, instead of from the table/container?

 

[Brinx]

My apologies for the giant wall of text that this post has turned into. I hope people find the patience to read it all!

DrClaude: the minimum radius of curvature of the chain is a lot smaller than the radius of curvature that is observed in the 'loop' that forms. I would not expect it to be a relevant factor in the behaviour of the system.

John: Thank you for registering to PF and joining in the discussion. While I appreciate that the reaction force plays a role in the distribution of translational and rotational kinetic energy of the link that leaves the pile, I do not quite follow the line of reasoning that comes after that. In the published model, all chain links are lifted up and very quickly reach the chain's general velocity (the magnitude of which we assume to be constant over some period of time) - rotational energy is not considered separately in any step. Do you mean that the chain links leave the pile with a higher velocity due to the 'kick' effect (as opposed to the effect being absent) and thus reach a greater height than the lip of the container? The case remains that the chain, once clearing the lip, is initially pulled down. Somehow the links crossing the lip do not get accelerated downwards quite so quickly and have sufficient inertia to continue their upward motion for a while.

If I may, I would like to discuss a black box model for the situation. In the description of its expected behaviour, I partway follow the steps that were made in the paper. Looking at the figure attached to this post, I have adopted most of the symbols that are used in the paper. I have not used a variable h2 to denote the height the loop reaches above the container: rather, I have included a variable h3 (to avoid confusion) to indicate the height of the bottom of the black box above the chain links lying in the container, but that value can be set as close to zero as desirable. I leave the precise loop geometry unspecified and put a black box around that part.

Now, assuming that the chain has reached the phase where it is flowing along a stationary (stable) trajectory, its links are all moving at velocity v. All moving links of the chain move at this velocity, only their direction of motion is different at different points along the trajectory. If we consider the black box and the forces that act on its contents, we can say that both the chain segment entering it and the chain segment exiting it exert some vertical force T on its contents. These forces have to be tensional forces (chains do not transmit compressional forces - at least the type used in this experiment does not), and they have to be equal: if they were unequal, the contents of the black box would have a net torque acting on them resulting in an angular acceleration of its contents and a changing chain velocity. The other external force acting on the black box is gravity, acting on all the mass in the black box: F_g = M_bb * g = L * lambda * g. So, the sum of external forces acting on the black box is F_total = -2T -F_g = -2T - L * lambda * g.

Looking at the traffic in and out of the black box, we see a segment of chain entering it with an upward velocity and an equally long segment of chain exiting it with a downward velocity (after all, the mass inside the black box is constant over time). Per unit of time, mass M_in = v * lambda is entering the black box with vertical momentum P_in = v^2 * lambda. Mass M_out = v * lambda is exiting the black box with vertical momentum P_out = -v^2 * lambda. The change in momentum per unit of time is thus: P_out - P_in = -2 * lambda * v^2. This has to be equal to the external forces experienced by the black box:

2 * lambda * v^2 = 2T + L * lambda * g.

The tension force T can be calculated by considering the length of chain moving down from the black box to the ground. This entire segment moves at constant velocity v, but experiences a gravitational force of F_g1 = h1 * lambda * g. So the tension force T has to be equal to this (sum of forces on descending chain segment = zero).

Filling in the value for T, we get 2 * lambda * v^2 = 2 * lambda * h1 * g + L * lambda * g. Isolating the velocity term, we get v^2 = h1 * g + L * g / 2. This result relates the size of the loop (L being the length of chain in the black box) to the velocity of the chain.

To solve for v or L independently, we would need a separate piece of information besides what I've discussed here it seems.

 

[DrClaude]

DrClaude: the minimum radius of curvature of the chain is a lot smaller than the radius of curvature that is observed in the 'loop' that forms. I would not expect it to be a relevant factor in the behaviour of the system.

I'm sorry if I was not clear, but I was thinking at what happens at the last point of the chain under tension, in the container.

My suspicion is that the explanation they give works for the system they have devised, which the string of macaroni, but does not apply exactly to the original case of Mould. Ufortunately, I don't have access to the paper, so I can only guess from what they say in the video.

 

[A.T.]

The case remains that the chain, once clearing the lip, is initially pulled down. Somehow the links crossing the lip do not get accelerated downwards quite so quickly and have sufficient inertia to continue their upward motion for a while.

It might be, that it is not the angular momentum of the individual links, but their linear momentum perpendicular to the chain, that prevents them from taking the shortest route down. The chain in the box is coiled up, and has many bends. When you pull it, it straightens, so the links in the bends gain linear momentum perpendicular to the pull. That's why they don't follow the initial pull direction to the edge of the box, but jump up higher. Now, the straightening and lateral acceleration of the picked up links happens continuously. Such a lateral impulse to a section of a chain, would usually propagate as a wave. So maybe you need wave dynamics to model the phenomenon.

 

[voko]

I believe this is the article by Biggins and Warner: http://arxiv.org/abs/1310.4056

I wonder whether the anomalous force could be measured directly, say, by suspending the pot on a dynamometer?

 

[JollyOlly]

Chain fountain

The chain fountain seems at first sight to defy all the laws of physics and yet the explanation is reasonably simple. Many people have, however, made two unwarranted assumptions which have led them astray.

The first assumption is that the tension in the chain at the top of the short (rising) section is the same as the tension at the top of the long (falling) section. This is not the case.

The tension at the top of the short section is equal to the weight of the short section plus the force required to accelerate the bottom of the chain into motion. This can be written as λh₂g + λv² (where λ is the mass per unit length of the chain and h₂ is the height of the loop above the beaker.)

The tension at the top of the long section is just the weight of the falling section of the chain λh₁g + λh₂g (where h₁ is the height of the beaker above the floor.)

The sum of these two tensions must provide the centripetal force needed to cause the chain to turn the corner and it is easy to see that this is equal to 2λv². (The 2 is needed because the momentum changes direction completely.)

Putting all this together leads to the fundamental relation between h₂ and h₁ namely:

(2h₂ + h₁)g = v²

Now in order to get any further, we need to consider where the energy in the system comes from. It is clear that the rate of production of KE must be some fraction (k) of the rate of loss of PE. ie:

λv²/2 = kλh₁g

Using this equation to eliminate v² we find that

h₂ = h₁(k - 0.5)

In Steven Mould's experiment h₁ appears to be about 1.2m and h₂ is about 0.2m. This implies that v is about 4 ms^-1 and k is about 0.67.

This sounds very reasonable except that there is a well established (and perfectly correct!) theory that says that under a wide range of conditions, the efficiency of the process of picking up a chain cannot be more than 50% ie k cannot be more than 0.5!

This is where the second invalid assumption comes in. The theory referred to above assumes that each link in the chain is effectively in collision with the one that precedes it and under these circumstances, energy is inevitably lost. The assumption being made is that every link in the chain must either be at rest or moving with speed v.

The situation here is different. A close look at the slow motion videos shows that the links (or beads) in the chain unwind themselves smoothly from the pile - in effect accelerating gradually from rest to their final vertical speed v without loss of energy. But how can bead A be traveling faster than the bead B immediately behind it when they are fixed together? you might ask. Good question. The answer is that it is only the component of the velocities of the two beads in the direction of their mutual link which must be equal. When the beads unwind off the pile, bead A has a greater sideways component of velocity than bead B and can therefore be traveling faster even though they are linked together.

Fascinating!

 

[voko]

As shown in the article by Biggins and Warner, the tension at the top given by $\lambda h g + \lambda v^2$ is incompatible with the formation of the fountain.

The phrasing "sum of these tensions" is ambiguous. Tensions certainly are not summed; the tension at the top is just the tension at the top of either segment, it is one and the same. Again, as shown in the article, it is $\lambda v^2$, not $2 \lambda v^2$.

 

[Brinx]

That's a great post JollyOlly, and the line of reasoning is clear.

I'm wondering about the statement that the two tension forces (at the start of the arc and the end of the arc) can be unequal though: does this not imply that there is angular acceleration going on in the arc (because of a net moment), against the assumption that we're dealing with a stationary geometry and chain velocity? Or does it simply mean that the arc is not a circular one?

 

[JollyOlly]

Voko - I am afraid I do not agree with Biggins and Warner's analysis. If you just consider the forces on the arc at the top (assuming it is relatively short and therefore its own weight van be neglected in comparison with the weight of the rest of the chain), the two tensions I referred to both pull down on the arc and therefore the total force pulling down on the arc is indeed the sum of these two forces. This force is responsible for reversing the direction of motion of the chain whose rate of change of momentum is 2λv²

Brinx - You have an excellent point there and it is not easy to see exactly what effect this will have on the shape of the arc. If we assume that the loop is completely stable, then every bead follows exactly the same path as its predecessor at exactly the same distance from it - ergo it must be traveling at the same speed. (NB as I have pointed out, this is not the case with the beads rising out of the pot!) My analysis shows that the tension in the string at the top of the rising section is greater than the tension at the top of the falling section so the tension in the chain reduces as it goes round the loop. If we assume that the centripetal force is constant all the way round the arc (I am not entirely happy about this though), this would seem to imply that the curvature of the arc should increase. I must have another look at the video and see if this is the case!

 

[voko]

Voko - I am afraid I do not agree with Biggins and Warner's analysis. If you just consider the forces on the arc at the top (assuming it is relatively short and therefore its own weight van be neglected in comparison with the weight of the rest of the chain), the two tensions I referred to both pull down on the arc and therefore the total force pulling down on the arc is indeed the sum of these two forces. This force is responsible for reversing the direction of motion of the chain whose rate of change of momentum is 2λv²

Since you essentially count the same value of tension twice, you obtain twice the value. There is no disagreement between you and the articles author's in that.

So the magnitude of tension at the top is $\lambda v^2$, which you say must be equal to $\lambda g h + \lambda v^2$, which means $h = 0$ and there is no fountain.

 

[JollyOlly]

Please read my post again carefully and do the algebra for yourself. I agree that the average tension at the top is λv² but I repeat - the tensions at each end of the arc are not equal! Using the figures I gave in my post, the tension at the top of the rising section is 18λ while that at the top of the falling section is 14λ. λv² is 16λ.

 

[voko]

Please read my post again carefully and do the algebra for yourself. I agree that the average tension at the top is λv² but I repeat - the tensions at each end of the arc are not equal!

That is impossible, because that would be necessarily causing the arc to rotate, which is not happening.

 

[JollyOlly]

I agree that it seems impossible. What you are saying is that if the tensions were not equal, the beads along the string would accelerate and that therefore they would emerge from the arc faster (or slower) than they entered - an obvious error.

The answer is as follows. Each bead is subjected to two forces, one from the bead in front and one from the bead behind. I maintain that these forces are unequal in magnitude. They also differ in direction. Now I agree that the bead travels at a constant speed. So all that is needed to make this true is for the resultant of the two forces to be at right angles to the instantaneous velocity of the bead - which is, of course, exactly what is required.

 

[voko]

I agree that it seems impossible. What you are saying is that if the tensions were not equal, the beads along the string would accelerate and that therefore they would emerge from the arc faster (or slower) than they entered - an obvious error.

No, this is not what I am saying. What I am saying is that when the forces are not equal, the net torque acting on the arc is not zero. So it will have to rotate. The internal forces within the arc are irrelevant for this statement.

 

[JollyOlly]

Yes, I see your argument but I am not sure how best to counter it. If 'the arc' was a rigid body you could indeed deduce that it would undergo an angular acceleration - but the arc is not a rigid body; it is composed of individual beads acted on by internal forces and these are the only forces which are relevant. The concept of 'the net torque on the arc' is not sufficiently well defined. About what point are the torques to be measured (remember, the arc is not circular)

 

[voko]

Let $\vec r(s, t)$ be the position of a point in the arc. $s$ is the natural parameter of the curve, $t$ is time. Let $T(s, t)$ be the magnitude of tension. Then $T {\partial \vec r \over \partial s}$ is the force of tension. A small element of the arc is acted upon by two forces of tension at its both ends. At one end, it is $T (s) {\partial \vec r \over \partial s} (s)$. At the other it is $T (s + \Delta s) {\partial \vec r \over \partial s} (s + \Delta s)$. As $\Delta s$ is small, this is $T (s) {\partial \vec r \over \partial s} (s) + {\partial \over \partial s} \left( T {\partial \vec r \over \partial s} \right) (s) \Delta s$. The difference of these two forces is the net force acting on the small element, hence Newton's second law for it is $$ \lambda \Delta s {\partial ^2 \vec r \over \partial t^2} = {\partial \over \partial s} \left( T {\partial \vec r \over \partial s} \right) \Delta s $$ Because the velocity of the elements in the arc is always along the arc itself and is constant ($v$), ${\partial \vec r \over \partial t} = v {\partial \vec r \over \partial s}$ and that implies $$ \lambda v {\partial \over \partial t} \left( {\partial \vec r \over \partial s} \right) = {\partial \over \partial s} \left( T {\partial \vec r \over \partial s} \right) $$ Changing the order of differentiation: $$ \lambda v {\partial \over \partial s} \left( {\partial \vec r \over \partial t} \right) = {\partial \over \partial s} \left( T {\partial \vec r \over \partial s} \right) $$ so $$ {\partial \over \partial s} \left( T {\partial \vec r \over \partial s} - \lambda v {\partial \vec r \over \partial t} \right) = 0 $$ and using the constancy of speed again $$ {\partial \over \partial s} \left( T {\partial \vec r \over \partial s} - \lambda v^2 {\partial \vec r \over \partial s} \right) = {\partial \over \partial s} \left( \left[T - \lambda v^2 \right] {\partial \vec r \over \partial s} \right) = 0 $$ Thus, $$ \left[T - \lambda v^2 \right] {\partial \vec r \over \partial s} = \vec c $$ where $\vec c$ is some constant vector. Since the arc is curved, ${\partial \vec r \over \partial s}$ changes direction along the arc, so this equality can only hold when $$ T = \lambda v^2 $$ So tension is constant in the arc (no matter what its shape), and is given by $\lambda v^2$ as said earlier.

Note the treatment above does not apply to the vertical segments where the weight of the chain must also be taken into account.

 

[Brinx]

Note the treatment above does not apply to the vertical segments where the weight of the chain must also be taken into account.

What is a good way to determine along which part of the chain your derivation holds, in that case? Is there a specific condition by which we may define the start and the end of the arc?

 

[voko]

What is a good way to determine along which part of the chain your derivation holds, in that case? Is there a specific condition by which we may define the start and the end of the arc?

The very first equation includes only tension; that ignores the weight. It can be taken into account by adding $\lambda \Delta s \vec g$ to the right hand side of the very first equation, where $\vec g$ is the constant vector of acceleration due to gravity. This results in $$ {\partial \over \partial s} \left( \left[ T - \lambda v^2 \right] {\partial \vec r \over \partial s} \right) = - \lambda \vec g $$ or $$ {\partial T \over \partial s} {\partial \vec r \over \partial s} + \left[ T - \lambda v^2 \right] \kappa \vec n = - \lambda \vec g $$ where $\kappa$ is curvature and $\vec n$ is the vector normal to the curve. Under the assumption that $v^2 \kappa \gg g$ we can ignore the right hand side term, and that brings us back to the previous derivation. This is the same assumption Biggins and Warner had. If, on the other hand, curvature is small, then we can ignore the second term on the left hand side, which gives us an essentially vertical path with tension growing linearly.

 

[JollyOlly]

Voko - the proof you submit leads to the, perfectly correct equation

[T−λv²]∂r/∂s=c

Now ∂r/∂s is the rate at which the vector r changes with distance along the arc s. Since the proof you quote is usually to be found in textbooks in the chapter on motion in a circle, it is almost always assumed without saying that this is constant. But as I have pointed out several times, the arc we are talking about is not circular. What this means is that ∂r/∂s is not constant. And if ∂r/∂s is not constant, neither is T.

 

[voko]

Voko - the proof you submit leads to the, perfectly correct equation

[T−λv²]∂r/∂s=c

Now ∂r/∂s is the rate at which the vector r changes with distance along the arc s. Since the proof you quote is usually to be found in textbooks in the chapter on motion in a circle

You are jumping to conclusions. I derived equations for the steady motion of a chain not affected by external forces. That has nothing do with the circular motion of a particle, which is "usually to be found in textbooks".

it is almost always assumed without saying that this is constant. But as I have pointed out several times, the arc we are talking about is not circular. What this means is that ∂r/∂s is not constant.

I did not assume it was constant. I said explicitly "Since the arc is curved, $\partial \vec r \over \partial s$ changes direction along the arc", which then implies that "this equality can only hold when $T = \lambda v^2$". Note also that due to natural parametrization the magnitude of $\partial \vec r \over \partial s$ is 1, so if we dot-multiply the equation with itself, we obtain $(T - \lambda v^2)^2 = c^2 = \mathrm {const}$, which implies that $T = \mathrm {const}$ without any assumptions on curvature.

 

[JollyOlly]

While I still don't quite follow your logic, Voko, I can see that for a chain moving in an arc of a circle of any radius, the tension which is as a result of the necessary centripetal forces is equal to λv² and - crucially - it is not dependent on the radius.

If you imagine a cowboy lassoo being whirled in a circle, the tension in the rope is λv² whatever the radius of the loop.

If, however, we were to take this formula T = λv² to be valid at all times and under all circumstances, it would follow that any rope, even one moving in a straight line! would have to have this tension in it! This is clearly absurd.

So there is something in your analysis which is not appropriate to the circumstances we are talking about.

Now I am not competent to follow your mathematics in detail but somewhere inside it I believe you have made an unwarranted assumption. My gut feeling is that it relates to the directions of the r vector and the tension vectors.

When a rope is moving in a circle at constant speed, it is natural to assume that these are in the same direction. But as I have pointed out before, the beads do not have to move in the direction in which they are pulled.

Notwithstanding the detailed mathematics of the motion of the arc (which I freely confess is beyond my ability), I believe that the experimental evidence is on my side. In Mould's video, the loop appears to be about 0.2m high and the height of the beaker above the floor is about 1.2m. (These figures are consistent with those quoted in Baggins and Warner's paper). The weight of the falling section of the chain is λ(1.2 + .2)g = 14λ. Since I think we can all agree that this section of the chain is traveling in a straight line at constant speed, the tension in the chain at the top of this section must be 14λ and, according to Voko, Baggins and Warner, this is the tension in the arc. The speed of the chain must therefore be √14 or 3.7 ms^-1.

According to my theory, the tension in the arc varies from 14λ at one end to 18λ at the other with a mean value of 16λ from which I deduce that the approximate speed of the chain will be √16 or 4.0 ms^-1.

Now the video shows 50m of chain emptying in 12s. ie a speed of 4.2 ms^-1.

I rest my case.

 

[voko]

If, however, we were to take this formula T = λv² to be valid at all times and under all circumstances, it would follow that any rope, even one moving in a straight line! would have to have this tension in it! This is clearly absurd.

I have stated a few times that the formula is valid only in particular circumstances: (1) motion is steady; (2) external forces are negligible; (3) the shape is curved.

So there is something in your analysis which is not appropriate to the circumstances we are talking about.

You are jumping to conclusions again. The equations are entirely appropriate for the description of the arc formed by the chain, because conditions (1) - (3) are satisfied. It is not appropriate for the description of the chain in vertical segments, which I did say earlier.

Notwithstanding the detailed mathematics of the motion of the arc (which I freely confess is beyond my ability), I believe that the experimental evidence is on my side. In Mould's video, the loop appears to be about 0.2m high and the height of the beaker above the floor is about 1.2m. (These figures are consistent with those quoted in Baggins and Warner's paper). The weight of the falling section of the chain is λ(1.2 + .2)g = 14λ. Since I think we can all agree that this section of the chain is traveling in a straight line at constant speed, the tension in the chain at the top of this section must be 14λ and, according to Voko, Baggins and Warner, this is the tension in the arc. The speed of the chain must therefore be √14 or 3.7 ms^-1.

You obviously did not understand the paper by Biggins and Warner. They show that tension and weight are not the only forces present, so your derivation is not in accord with Biggins and Warner. Me, I have only shown that tension in the arc is constant, I have not related that to the heights of vertical segments.

Not to mention that the height of beaker above the floor is greater than 1.2 m, it is most likely greater than 1.5 m, which makes your argument moot.

All I can recommend at this stage is to read the paper and read it carefully. You are disagreeing without understanding what you are disagreeing with.

 

[JollyOlly]

I thank you for clarifying the difference between our two theories and it would appear that the main difference between them is in the different predictions for the speed of the chain. I believe that Baggins and Warner would predict a speed of √ (h₁ + h₂)g whereas I predict a speed of √ (h₁ + 2h₂)g

Would anyone like to do some accurate experiments?

 

[AlephZero]

I have stated a few times that the formula is valid only in particular circumstances: (1) motion is steady; (2) external forces are negligible; (3) the shape is curved.

I don't disagree with your math given those assumptions, but ignoring the weight of the chain in the circular part of the motion seems just wrong. You could estimate the relative size of the weight and the tension, from the kinematics of the real world experiment.

Since the actual shape of the chain is a continuous curve, not an arc joined to two straight lines, it makes no physical sense to suddenly ignore the weight at the point where the curved part is assumed to start.

Throwing a different thought into the ring here, it seems reasonable that an idealized description of the motion will be a steady state solution, though the actual experiment shows a lot of "random" motion around that steady state, presumably from the "random" coiling of the chain from the pot. But in the actual experiment, the initial motion is not at all steady state. It would be interesting to see if it is possible for the fountain not to develop, for different initial conditions - e.g. start with some chain hanging over the edge of the pot (or over a light frictionless pulley) before releasing it.

It could be that the "balls on a string" experiment could create a fountain for the correct initial conditions, which might be rather different from the other chains - e.g. a very different curvature at the top, either smaller (and impractical, since the chain must fall not back into the pot) or larger (and not tested, since the experimenter didn't launch the chain with enough horizontal velocity).

Another thought: there seems an analogy with a water siphon here - though there are some obvious differences in the cause of the forces acting on the chain, or fluid.

 

[Brinx]

I don't disagree with your math given those assumptions, but ignoring the weight of the chain in the circular part of the motion seems just wrong. You could estimate the relative size of the weight and the tension, from the kinematics of the real world experiment.

That's what was bothering me a bit too - it is why I considered the whole curved part of the trajectory as a black box in a previous post. Then again, I did assume the tension at both ends of that segment to be constant and I am still not quite convinced one way or the other about that.

As the height of the loop seemed to be around 0.14 times the height of the pot above the floor (so the length of chain in that segment would be at least 0.28 times the length of the 'free-hanging' part) as described in the paper, it does look like the force of gravity plays a significant role in the force balance on that segment.

 

[voko]

I don't disagree with your math given those assumptions, but ignoring the weight of the chain in the circular part of the motion seems just wrong. You could estimate the relative size of the weight and the tension, from the kinematics of the real world experiment.

From the video, the radius of curvature is about 3 cm, and the speed is about 5 m/s. That makes normal acceleration in the arc about 833 m/s², a lot more than the gravitational acceleration. The uncertainty in the radius of just 1 cm is greater than the contribution of gravity, and so is the uncertainty of 1 m/s in speed. The fluctuation in the radius of curvature due to the clearly visible instabilities in motion will have a greater effect than gravity, so taking the smaller effect into consideration while ignoring the bigger seems strange to me.

 

[JollyOlly]

Since the actual shape of the chain is a continuous curve, not an arc joined to two straight lines, it makes no physical sense to suddenly ignore the weight at the point where the curved part is assumed to start.

I think you have an interesting point here. If you look at Mould's video closely you will see that the rising part of the chain is fairly straight; then the chain makes a sharp right angle bend followed by a more gradual arc into the falling section. Now all of us (myself included) have been assuming that the chain can be divided into three sections - straight up, arc, straight down. Perhaps we should consider a model which is divided into four sections - straight up, sharp 90deg curve, moderate 90deg curve, straight down. Would that make any difference to your analysis Voko?

 

[AlephZero]

From the video, the radius of curvature is about 3 cm, and the speed is about 5 m/s.

OK, so we can use that as a basis for formulating a more controlled situation which could also be done as an experiment.

Consider the chain running over a frictionless pulley of radius r, at constant speed v, and find the conditions for the chain to "lift off" from the pulley. I expect that would also shed light on the difference between the "macaroni" and "balls on a string" experiments.

 

[voko]

Consider the chain running over a frictionless pulley of radius r, at constant speed v, and find the conditions for the chain to "lift off" from the pulley.

Lift off meaning it is no longer acted on by any force from the pulley? How is that different from my previous analysis?

 

[voko]

Perhaps we should consider a model which is divided into four sections - straight up, sharp 90deg curve, moderate 90deg curve, straight down. Would that make any difference to your analysis Voko?

If we keep ignoring gravity, that does not affect anything. Tension is still constant. If we want to take gravity into account, that is no longer true. Tension will depend on location in the chain. The important question then is whether tension at the ends of the arc, whatever the arc is, but provided that the ends are at the same height, is the same. That I am not sure about generically yet (even though I am inclined to think so, intuitively). Perhaps we could agree on some particular shape for the arc and see whether that is the case for that shape.