Extremely confused on finding eigenvectors

[Jorge Cantu]

Extremely confused on finding eigenvectors? Below I have a picture that gives the matrice and the eigenvectors. How did the solution find these eigenvectors??
i.e. the eigenvalues are 7 and -2

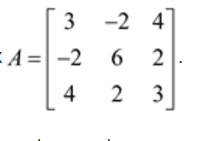
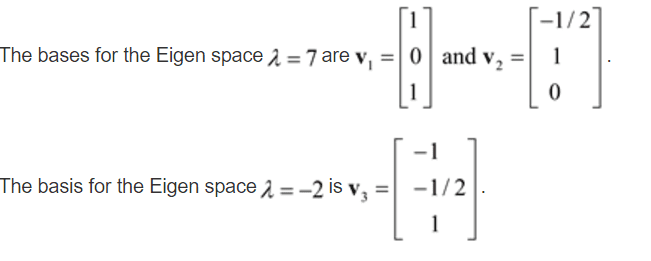
IMAGE LINKS
http://tinypic.com/r/2liii68/9
http://tinypic.com/view.php?pic=2liii68&s=9#.VkY_YfmrSUk

 

[mathwonk]

an eigenvalue for a matrix A is a number c such that the matrix A-cI is singular. So to find them we set the determinant of that matrix equal to zero and solve the resulting cubic equation if we can. Then afterwards, we have the numbers c that work, and using each one in its turn we actually find the kernel vectors of the matrices A-cI. Remark: Since the matrix is symmetric about the main diagonal you are guranteed to have 3 independent eigenvectors, even if some of the eigenvalues are repeated. So you have to know how to take determinants, and then you have to know how to solve a homogeneous system.

 

[WWGD]

You can also see it in the equivalent sense that , for a matrix/operator A, an eigenvalue $\lambda$ is the set of solutions for $\lambda$ to the equation :

$Ax= \lambda x$ (There may be no Real solutions or solutions over fields that are not algebraically closed. For Reals, this may be the case for square matrices of even dimension).

You can then expand , like Mathwonk said, the polinomyal $Det(A- \lambda I )x =0$ using , e.g., cofactor expansion and then find the roots , if any (when the base field is not algebraically closed.)

Once you find the eigenvalues, the eigenvectors are a basis for the nullspace of the above equation. Note that the collection of eigenvectors forms a subspace of the domain.