Failing in Analyzing these (unusual) circuits

[PhiowPhi]

I'm studying more (odd) circuits, where Kirchhoff law's would fail because of a magnetic field being part of a circuit, and it's flux is changing.
For example this circuit:

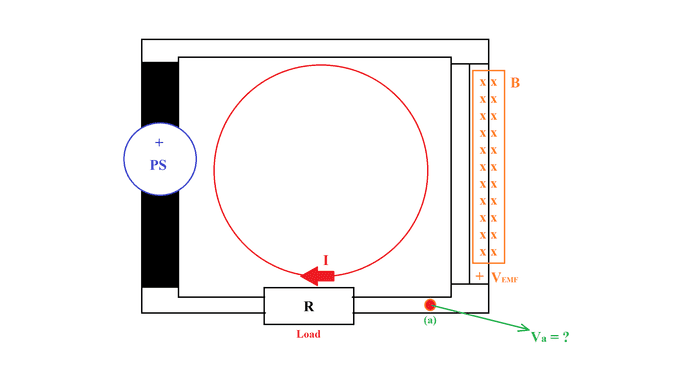
PS($V_P$)is an external power source connected to the circuit, where there is a wire that an external magnetic field is changing, the change in($B$) is negative, therefore inducing an EMF($V_E$) is positive:

$V_E$ = -$\frac{ \Delta (-B)A}{ \Delta t}$

The wires(two of them) the right hand one being inside a magnetic field, the other isn't are split in a way to reduce Eddy currents the black line in between is limitation/airgap.

I know that the direction of current is correct, as diagrammed. However, at point (a) what would be the total voltage there? What voltage would the load(R) see(or receive for a better word,even though it's voltage we're talking about, ...)? Is it simply $V_P$ + $V_E$?
It's odd to figure out without KVL.

It might be much easier to apply the magnetic field on both parallel wires like so:

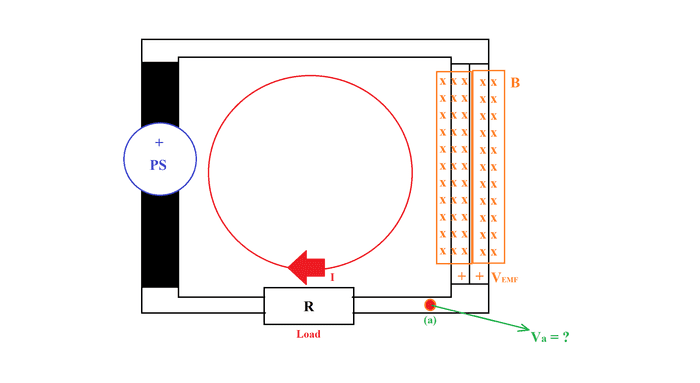
Now, we could assume the induced EMF to larger due to the area increase at the same given time, at the same change of magnetic field, here it's intuitive for me to assume the voltage would be $V_P$ + $V_E$.

Also, like to add for the first diagram it's only two wires but what if there are a lot more wires on the left side(not inside the magnetic field)?

 

[Jeff Rosenbury]

I = V_PS÷R

The magnetic circuit is shorted out and thus contributes nothing.

Or the magnetic circuit provides whatever you want, since it is not well defined. We really can't eliminate the eddy current, then drop a voltage across a 0Ω wire.

In a real circuit, there would be an eddy current traveling through the (non-magnetic) wire which would cause a small voltage equal to the eddy current times the wire's resistance. (I'll call that V_wire.) That would add to V_PS. (V_a=V_PS+V_wire)

 

[PhiowPhi]

I guess the second intuitive question would be: Why would the magnetic sub-circuit short? Given a load with finite resistance.
Why wound't the voltages add up? If there is already a small voltage due to Eddy currents( equal to I(Eddy's)xR) that add up the V_PS.

 

[Jeff Rosenbury]

It's nice to see you thinking. Having a deeper understanding than just grinding numbers will serve you well.

The magnetic sub-circuit can be modeled as the secondary half of a one turn transformer with a wire shorting the terminals. Since, for circuit analysis, wires are considered shorts with 0Ω, it shorts with an infinite current. (You can stretch the model by adding wire resistances and eddy currents to get an answer.)

In your second drawing, the wires could be modeled as two secondary transformers. Those would not be shorted.

It's important to understand that circuit analysis is a model, not reality. There are conditions where it breaks down. For example it is not great for distributed transmission lines. (It can be made to work by lumping elements, but there are better models.)