SUMMARY
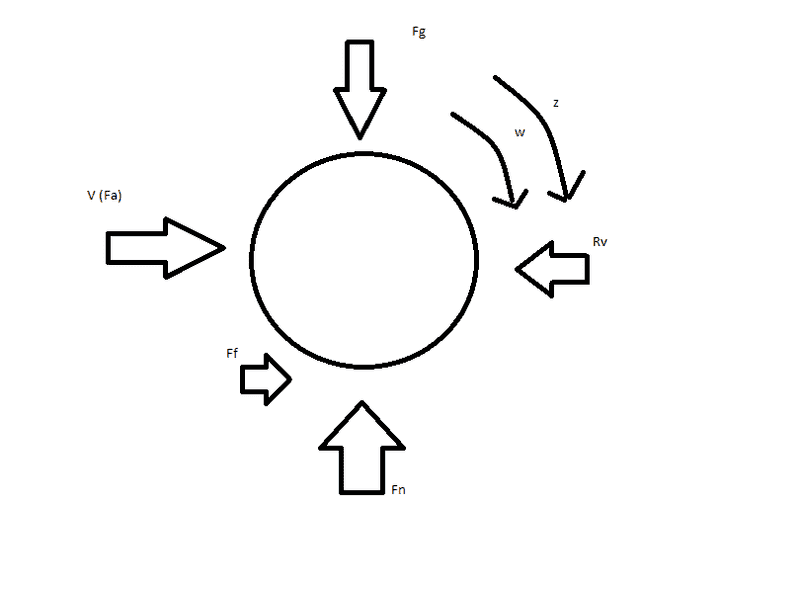
This discussion focuses on the forces acting on a rear-wheel drive (RWD) car's wheel during acceleration. The friction force from the road acts to the right, while the reaction force from the car acts to the left, both equal in magnitude. The torque applied to the wheel is influenced by the angular acceleration and the wheel's angular inertia, with a non-zero inertia resulting in a net torque that accelerates the car. The conversation emphasizes the importance of accurately representing forces in a free body diagram, specifically excluding forces generated by the wheel itself.
PREREQUISITES
- Understanding of Newton's laws of motion
- Familiarity with torque and angular acceleration concepts
- Knowledge of free body diagrams in physics
- Basic principles of vehicle dynamics
NEXT STEPS
- Study the principles of torque and angular inertia in detail
- Learn about free body diagram construction and analysis
- Explore the effects of rolling resistance and aerodynamic drag on vehicle performance
- Investigate the dynamics of rear-wheel drive systems in automotive engineering
USEFUL FOR
Automotive engineers, physics students, and anyone interested in understanding the dynamics of vehicle acceleration and the forces acting on wheels.