- #1
rudransh verma
Gold Member
- 1,067
- 95
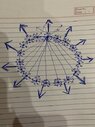
If there is a spherical conductor like this with excess charges on its surface then this is the field it sets up. Each e- would have there own radial field of lines. And all the e-s would exert a force on each charge and the net field on each charge and thus net force would be zero. All the e-s will be at rest. I tried to show this net effect of all field vectors on one top centre charge.
If I am correct then i want to ask what does it mean when we say the electric fields (vectors) are perpendicular to the surface of a charged conductor. Which field is this? Is this the net field vector at each point on the surface due to all the charges. Or is this field due to single e- that is perpendicular.
If I am correct then i want to ask what does it mean when we say the electric fields (vectors) are perpendicular to the surface of a charged conductor. Which field is this? Is this the net field vector at each point on the surface due to all the charges. Or is this field due to single e- that is perpendicular.
Attachments
Last edited: