- #1
ttiger2k7
- 58
- 0
[SOLVED] Field of long cylindrical shell conductor
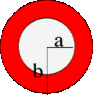
Shown above is the cross-section of a long cylindrical shell conductor of inner radius a=4.00 cm and outer radius b=7.00 cm which carries a current into the page.
The current density J (current/area) is uniform across the shell from r=a to r=b and has the magnitude J=3.6E3 A/m2 where r is the distance from the axis of the shell. (The magnitude of the total current carried by the conductor is thus given by I=J*π*(b2-a2)=37.3 A.)
(a) Find the magnitude of the magnetic field at r=2b=14 cm.
(b) Find the magnitude of the magnetic field at r=(a+b)/2=5.5 cm (halfway between the two shells).
(Hint: how much current is enclosed by the Amperian loop in each case?)
B = (uIr)/(2pi*R^2) (inside conductor, r<R)
B = (uI)/2pi*r (outside conductor r>R)
where u = 4*pi*10^-7
I already solved for part a, getting 5.33E-5 T using the second relevant equation.
But when I used the first relevant equation for part 1, I got 8.4 E-5 which I found out isn't correct. Here's how I did it:
(u*.055*37.3)/(2*pi*(.07^2)) = 8.4E-5 T.
What am I doing wrong?
Homework Statement
Shown above is the cross-section of a long cylindrical shell conductor of inner radius a=4.00 cm and outer radius b=7.00 cm which carries a current into the page.
The current density J (current/area) is uniform across the shell from r=a to r=b and has the magnitude J=3.6E3 A/m2 where r is the distance from the axis of the shell. (The magnitude of the total current carried by the conductor is thus given by I=J*π*(b2-a2)=37.3 A.)
(a) Find the magnitude of the magnetic field at r=2b=14 cm.
(b) Find the magnitude of the magnetic field at r=(a+b)/2=5.5 cm (halfway between the two shells).
(Hint: how much current is enclosed by the Amperian loop in each case?)
Homework Equations
B = (uIr)/(2pi*R^2) (inside conductor, r<R)
B = (uI)/2pi*r (outside conductor r>R)
where u = 4*pi*10^-7
The Attempt at a Solution
I already solved for part a, getting 5.33E-5 T using the second relevant equation.
But when I used the first relevant equation for part 1, I got 8.4 E-5 which I found out isn't correct. Here's how I did it:
(u*.055*37.3)/(2*pi*(.07^2)) = 8.4E-5 T.
What am I doing wrong?