Find di/dt and dr/dt for a DC circuit with indepedent current source

[Xhendos]

Homework Statement

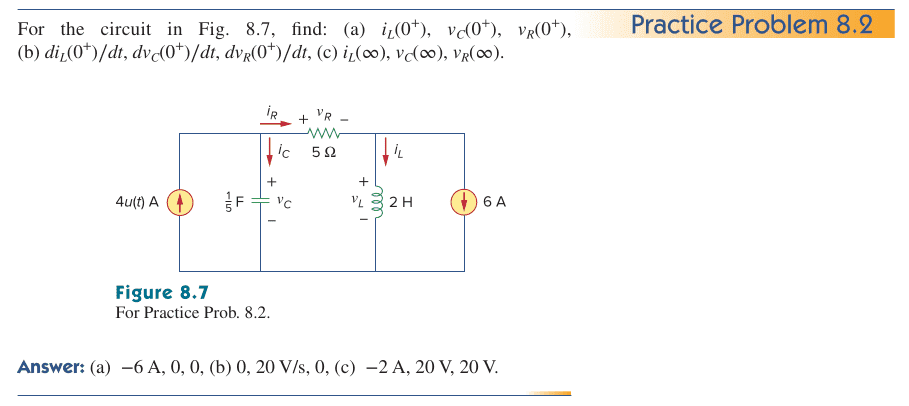
For the circuit in Fig. 8.7, find: (a) i L (0 + ), v C (0 + ), v R (0 + ),
(b) di L (0 + )∕dt, dv C (0 + )∕dt, dv R (0 + )∕dt, (c) i L (∞), v C (∞), v R (∞).

Relevant Equations

I = C dv/dt
V = L di/dt

Dear PF,

I am trying to solve practice problem 8.2. I am stuggling with part B of the question which asks us to find diL(0+)/dt, dvC(0+)/dt and dvR(0+)/dt.

My attempt can be seen below. Before t=0 the 4A current source is not present and thus it is an open circuit. A capacitor acts as an open circuit to DC and an inductor acts as a short circuit to steady-state DC conditions and thus that is why schematic for part A of the question looks like that. Using this schematic I find that iL = -6A and both vC and vR are 0V. This matches the answer of the book.

However, for part B of the question, I did manage to find dv/dt by using KCL at node A and B and using the fact that the inductor cannot change its current abruptly, so for t = 0+ the inductor current is still -6A.

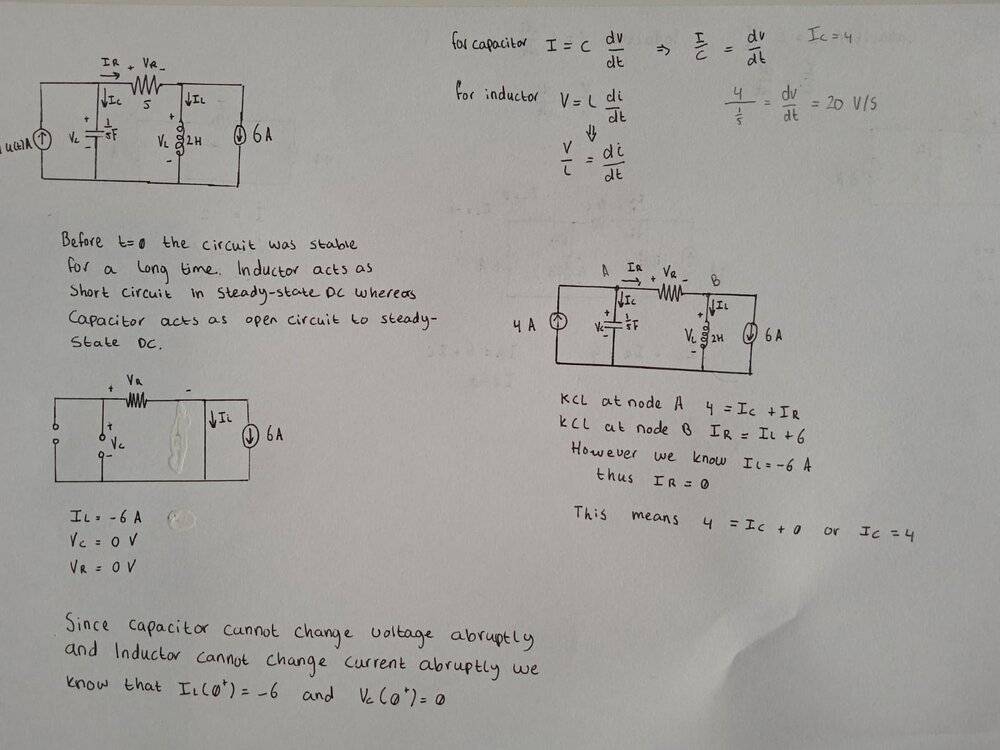
However, I am not quite sure how I can find di/dt and dr/dt. Can anyone give me a little hint here? I am stuck on this for quite a while.

 

[BvU]

the inductor cannot change its current abruptly, so for t = 0+ the inductor current is still -6A.

so what does that say about the (initial) $\displaystyle {di_L\over dt}$ ?

 

[Xhendos]

so what does that say about the (initial) $\displaystyle {di_L\over dt}$ ?

Right! Since the current iL does not change between interval 0- and 0+ the derivative at that point in time is 0! You are right. How about the resistor? Can we proof that current iR is 0 such that there is no potential voltage across the resistor its derivative and no current flows at t=0+ through the resistor?

 

[BvU]

there is no potential voltage across the resistor its derivative and no current flows at t=0+ through the resistor?

You found $V_R(0^+)$ in part (a). For the current the capacitor can swallow at $t=0^+$ there is (only theoretically) no limit: the current source is supposedly ideal and pumps in 4A, thereby determining $\displaystyle {{dV_C\over dt} \left (0^+\right )}$ according to what you said yourself:

The righthand side of the circuit doesn't interfere with this (the inductor does not like sudden changes in current).

But now comes the hard bit: $\displaystyle {{dV_R\over dt}\left (0^+\right )}$.
Charles' book answer is 0. What do you think ?

This assumption is indeed necessary.
But, different from 8.1, I don't see it in the problem statement ...