Find magnetic flux density(B) via vector potential(A)

[baby_1]

Hello
As you know we can find the flux density (B) via vector potential with this equation

So with this equation and solution at first i try to find vector potential completely then use above equation

Problem:

Solution:

my approach:

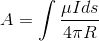
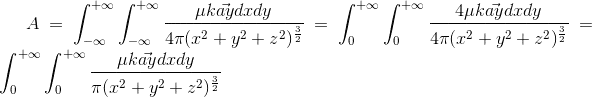
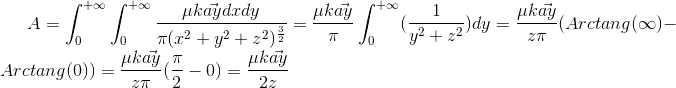
now we use curl A to find B

we find that

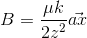
but it is different form the book soltuion

what is my problem and wrong?

Thanks

 

[TSny]

my approach:

Note how you wrote R in terms of x, y, z. Is the 3/2 power correct?

 

[baby_1]

Thanks Dear Tsny.you'r correct
as i want to solve the new integral

a new problem appears

for example if i want to calculate the inner integral the integral going to be infinite.

Ln(infinite)=infinite

now how can solve this problem?
Thanks

 

[TSny]

Yes, the integral is infinite. It's similar to trying to finding the potential V of an infinite line charge by integrating dV = k dq/r. Here you will also get a divergent integral. This is due to the charge distribution extending to infinity while at the same time trying to take the potential to be zero at infinity. (Note kdq/r goes to zero at infinity.)

You can avoid the problem by not demanding that the potential be zero at infinity. For example, in the infinite line charge example, you can pick an arbitrary point in space to be zero potential. The potential at other points is then defined relative to this chosen point.

You can try a similar trick for the vector potential. Thus define A as the following (with constants left out)

$$\int_{0}^{\infty} \int_{0}^{\infty} \frac{1}{\sqrt{x^2 +y^2+z^2}} dx dy - \int_{0}^{\infty} \int_{0}^{\infty} \frac{1}{\sqrt{x^2 +y^2+z_0^2}} dx dy$$

$z_0$ is just an arbitrarily chosen point on the z axis where you are taking A to be 0.

Each integral individually diverges. But if you combine the integrals before letting the upper limits go to infinity, you get a finite result that you can use for A.

 

[paranormal]

for your question. Without more details, it's difficult to determine exactly where your mistake may be. However, here are some possible reasons for why your solution may be different from the book's:

1. Different methods or equations used: There are different ways to calculate the magnetic flux density using the vector potential. It's possible that you are using a different method or equation than the one used in the book, which could result in a different solution.

2. Mistake in calculation: It's possible that you made a mistake in your calculation. Double check your steps and calculations to ensure they are correct.

3. Different assumptions or conditions: The solution in the book may be based on certain assumptions or conditions that are not stated in the problem. Make sure you are using the same assumptions and conditions in your solution.

4. Different coordinate systems: The solution in the book may be using a different coordinate system than the one you are using. Make sure you are using the same coordinate system in your solution.

It's important to carefully review your approach and calculations to identify where the discrepancy may be coming from. If you are still unsure, it may be helpful to consult with a colleague or mentor for further guidance.