- #1
Hasan2022
- 3
- 0
Hi,
I am willing to simulate a 3D ferrite bar transmitter and reciever where coupling coefficient k and Bt magnetic flux density on the each side uses the finite element method for solving partial differential equations.
The Magnetic Fields module has equation (jωσ − ω2ε0εr)A + ∇ × H = Je,
which enables calculation of magnetic field distribution B = ∇ × A, where ω is the angular frequency, σ is the electrical conductivity, ε0 is the permittivity of vacuum, εr is the relative permittivity, A is the magnetic vector potential, H is the magnetic field intensity, B is the magnetic flux density, and Je is the external current density.
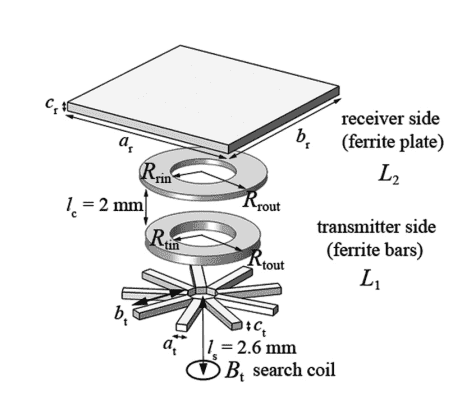
In my research AC/DC Module, Magnetic Fields need to used for simulation of magnetic flux density and the coupling coefficient in 3D numerical models. Coil Current Calculation, and Frequency Domain for each of the transmitter and receiver coil need to use for studies of a problem in Comsol Multiphysics.Two parameters, the coupling coefficient k and magnetic flux density on transmitter side Bt for stray magnetic fields were used in measurements. The first parameter k was used to analyze the different ferrite core geometries. The second parameter Bt was used to analyze the optimal geometries of ferrite bars in terms of magnetic shield.Two models are required in Comsol Multiphysics, where in the first model simulated self-inductance of the transmitter coil L1, mutual inductance M, and magnetic flux density Bt. With the second model it should simulated self-inductance of the receiver coil L2.Kindly see the geometry made of n = 9 ferrite bars on the transmitter side and ferrite plate on the receiver side.
I am willing to simulate a 3D ferrite bar transmitter and reciever where coupling coefficient k and Bt magnetic flux density on the each side uses the finite element method for solving partial differential equations.
The Magnetic Fields module has equation (jωσ − ω2ε0εr)A + ∇ × H = Je,
which enables calculation of magnetic field distribution B = ∇ × A, where ω is the angular frequency, σ is the electrical conductivity, ε0 is the permittivity of vacuum, εr is the relative permittivity, A is the magnetic vector potential, H is the magnetic field intensity, B is the magnetic flux density, and Je is the external current density.
In my research AC/DC Module, Magnetic Fields need to used for simulation of magnetic flux density and the coupling coefficient in 3D numerical models. Coil Current Calculation, and Frequency Domain for each of the transmitter and receiver coil need to use for studies of a problem in Comsol Multiphysics.Two parameters, the coupling coefficient k and magnetic flux density on transmitter side Bt for stray magnetic fields were used in measurements. The first parameter k was used to analyze the different ferrite core geometries. The second parameter Bt was used to analyze the optimal geometries of ferrite bars in terms of magnetic shield.Two models are required in Comsol Multiphysics, where in the first model simulated self-inductance of the transmitter coil L1, mutual inductance M, and magnetic flux density Bt. With the second model it should simulated self-inductance of the receiver coil L2.Kindly see the geometry made of n = 9 ferrite bars on the transmitter side and ferrite plate on the receiver side.