Discussion Overview
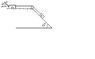
The discussion revolves around a physics homework problem involving two blocks on an inclined plane and a horizontal surface, focusing on calculating the magnitude and direction of a force P required to initiate motion. Participants explore the equations of motion, frictional forces, and the relationship between the angle θ and the force P.
Discussion Character
- Homework-related
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant presents the problem and initial calculations, expressing uncertainty about the angle θ needed for further calculations.
- Another participant asks for the equations derived from the problem to better understand the approach taken.
- A participant describes the forces acting on block A and block B, providing equations for normal force and tension, but acknowledges the need for the angle θ to solve for force P.
- Some participants suggest substituting variables to simplify the equations, indicating a method to express the relationship between P, θ, and other forces.
- There is a correction regarding the angle θ, clarifying that it is not 60 degrees but rather the angle made by force P on the horizontal.
- One participant notes that the derived equation allows for multiple values of θ, each corresponding to a unique value of P, raising the question of which θ minimizes P.
- A later reply suggests that the minimum value of P occurs when the sine function is maximized, indicating a relationship between θ and the sine function.
- Another participant expresses gratitude for the explanation but uses informal language, indicating a casual tone in the discussion.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the value of θ or the final expression for P, as multiple interpretations and approaches are presented. The discussion remains unresolved regarding the exact calculations and relationships between the variables.
Contextual Notes
There are unresolved assumptions regarding the angle θ and its impact on the calculations. The discussion reflects varying interpretations of the problem setup and the equations derived from it.