Find power of resistor and source in AC circuit

[Same-same]

Homework Statement

If an average power of 500W is dissipated in the 20Ω resistor, find V_rms, I _{S RMS}, the power factor seen by the source, and the magnitude of V_S
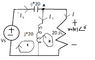
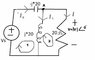
(Based on circuit in attached diagram)

Homework Equations

Pave= I_rms*V_rms*pf*\frac{1}{2}
Imaginary number referred to as "j", not "i".

The Attempt at a Solution

V_A=V
By a node equation at node A, we see that \frac{V}{20}= \frac{V_S}{-j*20}, so V = V_S \angle-90

Loop 1: (j*20-j*20)I_S -j*20I= V_S
By observation, I=V/20, so V=V_S\angle90.
Loop 2: (20+j*20)I-j*20I_S=0, so I_S= 1.41\angle135 *I
= 1.41\angle135 *\frac{V}{20}= 0.0705 V \angle135

Since I and V are in phase, the power across the resistor is 1
Solve for V:
500=V*\frac{V}{20}\frac{1}{2}, so V=\sqrt{20,000}=
100\sqrt{2}=141.4.

V_rms=\frac{V}{\sqrt{2}} =100,

Since V = 100\sqrt{2} I_S =7.05 *\sqrt{2} \angle135, so I _{S RMS} = 7.05

V=V_S\angle90, so V_S=V\angle-90
And I_S= 0.0705 V \angle135,
So power factor pf = cos(135-90)= 0.707

V_S=V\angle-90 = -141.4*j, so magnitude given by 141.4.

I think I got this right, but I just want to make sure.

 

[Same-same]

Just realized the diagram I attached was small, hopefully this one's easier to read.

 

[rude man]

Homework Statement

If an average power of 500W is dissipated in the 20Ω resistor, find V_rms, I _{S RMS}, the power factor seen by the source, and the magnitude of V_S
(Based on circuit in attached diagram)

Homework Equations

Pave= I_rms*V_rms*pf*\frac{1}{2}
.

Bad start.