Discussion Overview
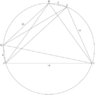
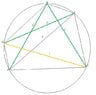
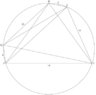
The discussion revolves around finding the sum of the lengths of the diagonals of a pentagon $PQRST$ inscribed in a circle, given specific side lengths. Participants explore various methods to derive the lengths of the diagonals and the overall sum, engaging in mathematical reasoning and conjecture.
Discussion Character
- Exploratory
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant proposes that the diagonals $PR$, $QS$, and $RT$ are equal and suggests they might all have a length of $12$, based on a visual guess and circumradius calculations.
- Another participant mentions applying Ptolemy's theorem multiple times to derive a set of equations relating the sides and diagonals of the pentagon.
- A later reply emphasizes the need to prove that $PR=12$ and provides a circumradius formula to justify the initial guess.
- Some participants express appreciation for the conjectures and calculations presented, while others challenge the need for proof of the guessed diagonal lengths.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correctness of the guessed diagonal lengths, and there is ongoing debate regarding the application of Ptolemy's theorem and the validity of the circumradius calculations.
Contextual Notes
The discussion includes various assumptions about the geometric properties of the pentagon and the rationality of the diagonal lengths, which remain unresolved. The reliance on visual guesses and circumradius calculations introduces uncertainty in the claims made.