Find the center of mass of a lamina

[paraboloid]

The boundary of a lamina consists of the semicircles y=\sqrt{1-x^2} and y=\sqrt{4-x^2} together with the portions of the x-axis that join them. Find the center of mass of the lamina if the density at any point is proportional to its distance from the origin.

I drew a graph that looks like this

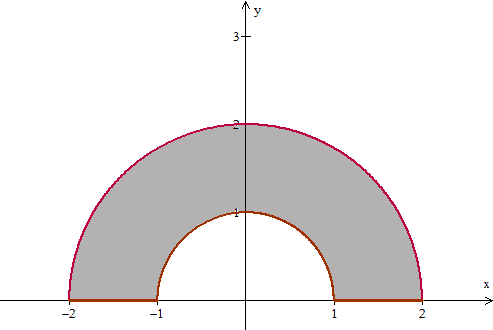
I know that polar coordinates are a good tool to use for circle type questions like this, but I've never encountered something like this before.
If anyone could just step me in the right direction, that would be great,
Thanks

 

[rock.freak667]

With composite objects like that, you can just consider the entire thing, and then subtract the smaller circle.

Your relevant equation should be

M \bar{y} = \int_M y dm

So start with a general circle of radius R.


If you consider an elemental section at an angle dθ, which has a mass dm and with length dr.

What is the mass of that element dm equal to ?

(I am assuming σ is the area density)

 

[paraboloid]

That is a very good strategy I overlooked. Thanks so much.

 

[Mark44]

To add a small bit to what rock.freak667 said, you don't need to solve for M_{\bar{x}}, since the x-coordinate of the center of mass will be somewhere along the y-axis (by the symmetry of the object and the density).