Find the correct value of the mean in the given problem

[chwala]

Homework Statement

See attached.

Relevant Equations

Statistics

Find the problem and solution below;

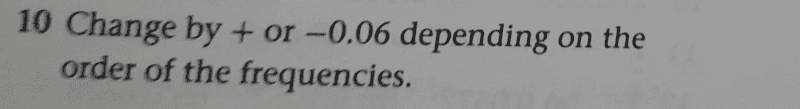
Now the part i do not seem to understand from the given solution is the negative value i.e to be specific $-0.06$
In my understanding we shall have $5$ possibilities with each giving the correct mean value of $3.48$ which implies $+0.06$ from the given value on the text unless they meant $3.48- 0.06=3.42$
They also did not indicate the correct value of the mean rather the difference.

My approach to the solution is as follows;

Consider the consecutive scores$1=12$ and $2=9$ then it follows that the correct value of the mean will be given by;

$(171-30)+1(9)+2(12)=174$

$\dfrac{174}{50}=3.48$


Consider the consecutive scores$2=12$ and $3=9$ then it follows that the correct value of the mean will be given by;

$(171-51)+2(9)+3(12)=174$

$\dfrac{174}{50}=3.48$


Consider the consecutive scores$3=12$ and $4=9$ then it follows that the correct value of the mean will be given by;

$(171-72)+3(9)+4(12)=174$

$\dfrac{174}{50}=3.48$

Consider the consecutive scores$4=12$ and $5=9$ then it follows that the correct value of the mean will be given by;

$(171-93)+4(9)+5(12)=174$

$\dfrac{174}{50}=3.48$

Consider the consecutive scores$5=12$ and $6=9$ then it follows that the correct value of the mean will be given by;

$(171-114)+5(9)+6(12)=174$

$\dfrac{174}{50}=3.48$

Of course i would appreciate any other better approach. Cheers guys.

 

[Office_Shredder]

What if, e.g, it says 5=9 and 6=12 and then you had to swap them (so the opposite direction of your post)

 

[FactChecker]

You could have used a variable, n, in your method:
Suppose the incorrect calculation included Incorrect=12n + 9(n+1) = 21n+9. Then the correct calculation would be Correct=9n+12(n+1) = 21n+12. The difference (removing the Incorrect and adding the Correct) would be -(21n+9)+(21n+12) = 3. That would change the final mean of the 50 samples by 3/50 = 0.06.
Now suppose the opposite mistake was made. A similar calculation says that the difference would be -3, giving a change of -3/50=-0.06.

 

[chwala]

What if, e.g, it says 5=9 and 6=12 and then you had to swap them (so the opposite direction of your post)

True, we shall have a mean value of $3.36$Thanks.

 

[chwala]

You could have used a variable, n, in your method:
Suppose the incorrect calculation included Incorrect=12n + 9(n+1) = 21n+9. Then the correct calculation would be Correct=9n+12(n+1) = 21n+12. The difference (removing the Incorrect and adding the Correct) would be -(21n+9)+(21n+12) = 3. That would change the final mean of the 50 samples by 3/50 = 0.06.
Now suppose the opposite mistake was made. A similar calculation says that the difference would be -3, giving a change of -3/50=-0.06.

@FactChecker smart move there...