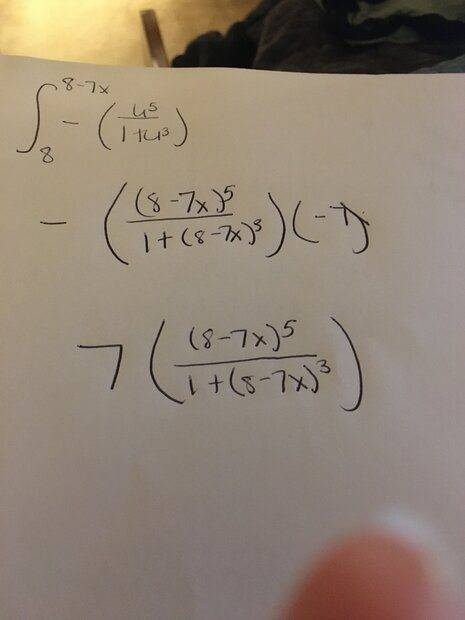SUMMARY
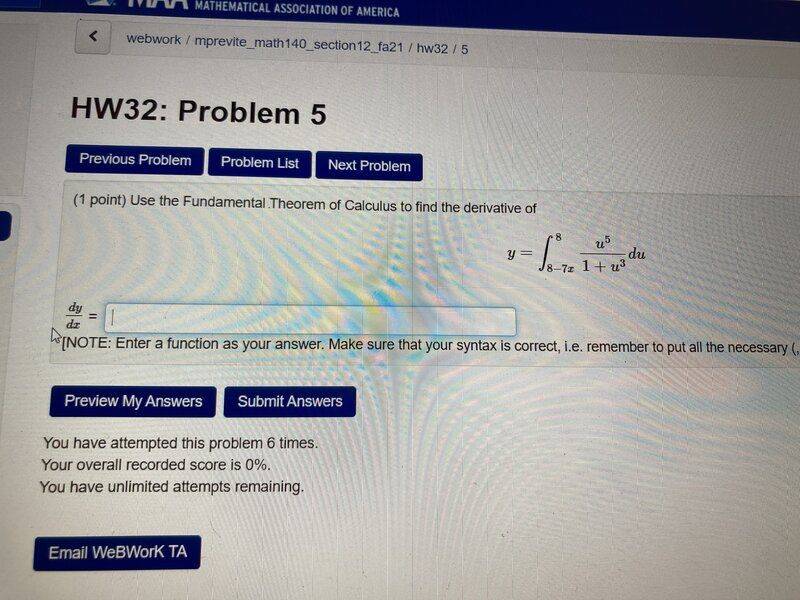
The discussion centers on finding the derivative of the function y = u^5/(1 + u^3) within the context of a definite integral from 8 to 8 - 7x. Participants highlight the importance of correctly interpreting the problem, emphasizing that the derivative must be taken of the definite integral rather than the function itself. Key issues identified include the omission of 'du' in the calculations and potential syntax errors in the input format, which could lead to incorrect results being flagged by software.
PREREQUISITES
- Understanding of calculus, specifically differentiation and integration.
- Familiarity with the chain rule and product rule in calculus.
- Knowledge of definite integrals and their properties.
- Experience with mathematical software or tools for inputting expressions correctly.
NEXT STEPS
- Review the process of finding derivatives of definite integrals.
- Study the application of the chain rule and product rule in calculus.
- Learn about common syntax requirements for mathematical software.
- Practice problems involving the differentiation of rational functions.
USEFUL FOR
Students and educators in calculus, mathematicians working with derivatives, and anyone using mathematical software for solving integrals and derivatives.