Find the magnitude of the electric force from 3 charges at vertices of a cube

[paulimerci]

Homework Statement

Question is posted below.

Relevant Equations

Coulomb law F_e = kq1q2/r^2

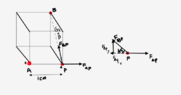
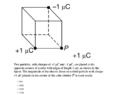
There are three charges with +1 μC and −1 μC, are placed at the opposite corners of a cube with edges of length 1 cm, and the distance from P to B is 1cm 2. I labeled them as A, P, and B, which is shown in the diagram below. Since we need to find the magnitude of the charge at point P and the charge at point P is +1 μC, it exerts an attractive force on point B and a repulsive force on point A. I've indicated the FBD below. Using Coulomb's law, we get
Fe=kq1q2r2
∑Fx=FBPcos45+FAP
∑Fx=91

∑Fy=FBPsin45
∑Fy=45.5N
Using Pythagorean we get,
Resultant magnitude of electric force = 101.7N
I did something wrong here. Can anyone point out where I made the mistake?
Thank you!

 

[TSny]

Are you sure that force $\mathbf{F}_{BP}$ has a nonzero x-component?

 

[paulimerci]

Are you sure that force $\mathbf{F}_{BP}$ has a nonzero x-component?

Does that mean F_BP cancels with F_AP since they are in opposite directions?

 

[paulimerci]

Are you sure that force $\mathbf{F}_{BP}$ has a nonzero x-component?

I got the answer, and I edited my answer in post #1.

 

[TSny]

Fe=kq1q2r2
∑Fx=FBPcos45+FAP
∑Fx=91

The equation $\sum F_x = F_{BP}\cos 45^o + F_{AP}$ is not correct.
Can you see that the vector $\mathbf{F}_{BP}$ is perpendicular to the vector $\mathbf{F}_{AP}$?

∑Fy=FBPsin45
∑Fy=45.5N

$F_{BP}\sin 45^o \neq 45.5 N$. What value did you get for $F_{BP}$?

Does the vector $\mathbf{F}_{BP}$ have a z-component as well as a y-component?
In your diagram, you didn't indicate the directions of the x, y, and z axes.

 

[paulimerci]

The equation $\sum F_x = F_{BP}\cos 45^o + F_{AP}$ is not correct.
Can you see that the vector $\mathbf{F}_{BP}$ is perpendicular to the vector $\mathbf{F}_{AP}$.$F_{BP}\sin 45^o \neq 45.5 N$. What value did you get for $F_{BP}$?

Does the vector $\mathbf{F}_{BP}$ have a z-component as well as a y-component?
In your diagram, you didn't indicate the directions of the x, y, and z axes.

Isn’t the $F_{BP} sin45$ perpendicular to the $F_{AP}$?
F_BP sin 45 = 31.8N

 

[TSny]

The key is to realize that the vector $\mathbf{F}_{BP}$ is perpendicular $\mathbf{F}_{AP}$.

If you see that the two vectors are perpendicular, then it should be easy to find the magnitude of their sum. You don't need to consider x, y, or z components.

 

[paulimerci]

The key is to realize that the vector $\mathbf{F}_{BP}$ is perpendicular $\mathbf{F}_{AP}$.

View attachment 326712
If you see that the two vectors are perpendicular, then it should be easy to find the magnitude of their sum. You don't need to consider x, y, or z components.

Thanks for the diagram. I can't visualize F_BP perpendicular to F_AP.

 

[TSny]

Thanks for the diagram. I can't visualize F_BP perpendicular to F_AP.

$\mathbf{F}_{BP}$ lies in the face of the cube that is shaded yellow.

The edge AP of the cube is perpendicular to the yellow face.

Imagine looking at the cube so that you are looking directly at the yellow face.

Imagine what the direction of $\mathbf{F}_{AP}$ would be in this picture.

 

[paulimerci]

$\mathbf{F}_{BP}$ lies in the face of the cube that is shaded yellow.

The edge AP of the cube is perpendicular to the yellow face.

Imagine looking at the cube so that you are looking directly at the yellow face.
View attachment 326713
Imagine what the direction of $\mathbf{F}_{AP}$ would be in this picture.

I think I understood what you said. So the magnitude of the electric force is 128N?

 

[TSny]

I think I understood what you said. So the magnitude of the electric force is 128N?

Please show the calculation that gave you this result.

What value did you get for $F_{AP}$?

What value did you get for $F_{BP}$?

 

[paulimerci]

Please show the calculation that gave you this result.

What value did you get for $F_{AP}$?

What value did you get for $F_{BP}$?

Ok.
$F_{AP} = 91N$
$F_{BP} = 91N$
Using Pythagorean, the net magnitude of electric force at point p is 128N.

 

[TSny]

$F_{AP} = 91N$

I'm not sure how you got 91 N rather than 90 N. The value of Coulomb's constant is $k = 8.99 \times 10^9$ Nm²/C².

$F_{BP} = 91N$

The distance between B and P is greater than the distance between A and P. So, shouldn't $F_{BP}$ be less than $F_{AP}$?

 

[paulimerci]

I'm not sure how you got 91 N rather than 90 N. The value of Coulomb's constant is $k = 8.99 \times 10^9$ Nm²/C².The distance between B and P is greater than the distance between A and P. So, shouldn't $F_{BP}$ be less than $F_{AP}$?

Yes, the distance between B and P is greater than the distance between A and P. I took $k = 9\times 10^9 Nm^2/C^2$
I did something wrong in calculating the distance.
$F_{BP} = 45.5 N$ and $F_{AP} = 91N$.
Thereby the magnitude of electric force at point P is 102N.

 

[SammyS]

Yes, the distance between B and P is greater than the distance between A and P. I took $k = 9\times 10^9 Nm^2/C^2$
I did something wrong in calculating the distance.
$F_{BP} = 45.5 N$ and $F_{AP} = 91N$.
Thereby the magnitude of electric force at point P is 102N.

Using $\displaystyle k = 9\times 10^9 \, \rm{Nm^2/C^2}$ rather than $\displaystyle 8.99\times 10^9 \, \rm{Nm^2/C^2}$ will give $F_{AP} = 90\, \rm N$

 

[paulimerci]

Using $\displaystyle k = 9\times 10^9 \, \rm{Nm^2/C^2}$ rather than $\displaystyle 8.99\times 10^9 \, \rm{Nm^2/C^2}$ will give $F_{AP} = 90\, \rm N$

I'm sorry I used $k= 9.1 \times 10^9 Nm^2/C^2$ that's how I got the answer for $F_{AP} = 91N$

 

[TSny]

$F_{BP} = 45.5 N$ and $F_{AP} = 91N$.
Thereby the magnitude of electric force at point P is 102N.

OK. You have the solution. Using k = 9.0 x 10⁹ Nm²/C² would give 101 N. But the data in the problem is stated to only one significant figure! Your answer is close enough to pick out the correct answer in the multiple choice.

 

[paulimerci]

OK. You have the solution. Using k = 9.0 x 10⁹ Nm²/C² would give 101 N. But the data in the problem is stated to only one significant figure! Your answer is close enough to pick out the correct answer in the multiple choice.

The answer is close to 100 N. Thank you @TSny for your great help!