Find the position vector of ##Q##

[chwala]

Homework Statement

see attached (highlighted in Red)

Relevant Equations

vectors

O level question; i used similarity would appreciate an easier approach for 2 marks.

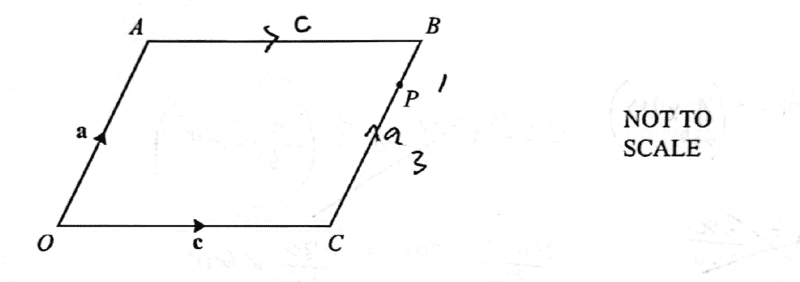
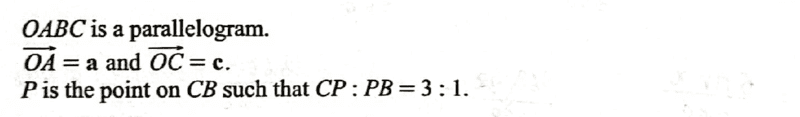
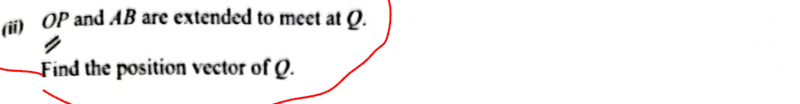
The ms solution (approach) is not clear to me. Here it is;

My approach; using similarity

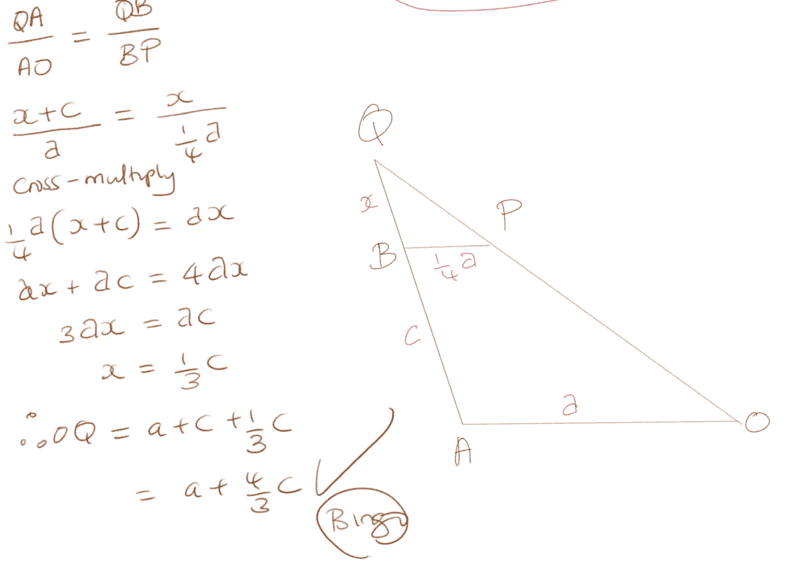
Any insight welcome its a 2 mark question- cannot seem to find easier way though i suspect reflection.

 

[anuttarasammyak]

 

[chwala]

View attachment 343313

...still not getting it. You mind giving some reason or thought. Thks.

 

[anuttarasammyak]

Triangle OPC and QPB are similar with ratio 3.

 

[SammyS]

Triangle OPC and QPB are similar with ratio 3.

And ΔQOA is similar to each of those two.