- #1
chwala
Gold Member
- 2,650
- 351
- Homework Statement
- see attached
- Relevant Equations
- total derivatives
see attached below; the textbook i have has many errors...
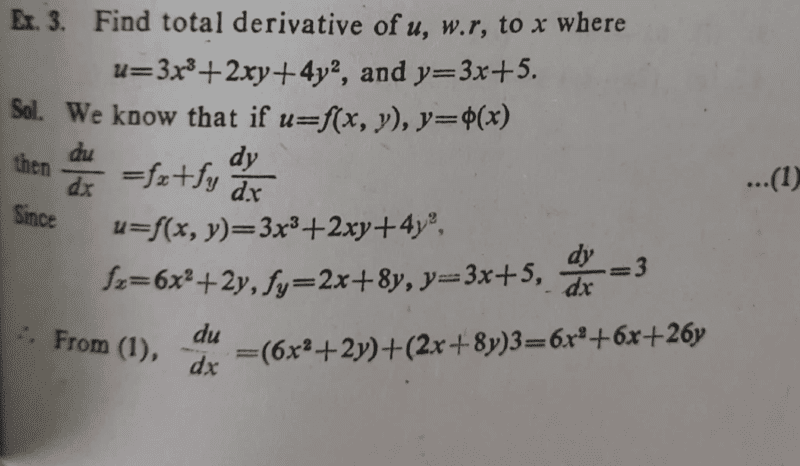
clearly ##f_x## is wrong messing up the whole working to solution...we ought to have;
##\frac {du}{dx}=(9x^2+2y)+(2x+8y)3=9x^2+2y+6x+24y=9x^2+6x+26y##
clearly ##f_x## is wrong messing up the whole working to solution...we ought to have;
##\frac {du}{dx}=(9x^2+2y)+(2x+8y)3=9x^2+2y+6x+24y=9x^2+6x+26y##
Last edited: