GLD223
- 14
- 7
- Homework Statement
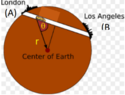
- The train will use gravity to traverse from point A to B, in your answer, use the gravitational constant g and R - the radius of the earth in your answer. Assume the earth's mass is uniform
- Relevant Equations
- ##L = T-V, KE(0) = 0, PE(0) = KE + PE##
I need to find the transit time of the train, from what I see online it should be independent of points A and B and should be roughly 42 minutes.
I started by looking at the energies and derived an ODE for the speed of the train to find the transit time but it seems to be wrong.
Also, I might need to use the Lagrangian since we learned it in the last lesson.
##M_earth := M##
##\rho = M/4/3 * \pi * R^3##
##M(r) = r^3/R^3 * M##
##T = 1/2 * m *(dx/dt)^2##
##U(0) = -mgR##
##U(r) = -mg/R *r^2##
I started by looking at the energies and derived an ODE for the speed of the train to find the transit time but it seems to be wrong.
Also, I might need to use the Lagrangian since we learned it in the last lesson.
##M_earth := M##
##\rho = M/4/3 * \pi * R^3##
##M(r) = r^3/R^3 * M##
##T = 1/2 * m *(dx/dt)^2##
##U(0) = -mgR##
##U(r) = -mg/R *r^2##
Attachments
Last edited: