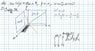SUMMARY
The volume of the region bounded by the planes defined by the equations 7x + 6y + 8z = 9, y = x, x = 0, and z = 0 can be calculated using multiple integration techniques. The correct setup for the triple integral is established as $$ \int_0^{\frac{9}{7}} \int_0^{\frac{9-7x}{6}} \frac{9-7x-6y}{8} dy dx $$, which accounts for the limits of integration based on the intersection points of the planes. The initial incorrect limits in the dy integral were identified as a source of error in the calculations. The final volume can be computed accurately using this corrected integral setup.
PREREQUISITES
- Understanding of multiple integration techniques
- Familiarity with the concept of bounded regions in three-dimensional space
- Knowledge of plane equations and their intersections
- Experience with evaluating triple integrals
NEXT STEPS
- Study the method of setting up triple integrals for volume calculations
- Learn about the geometric interpretation of multiple integrals
- Practice solving similar problems involving bounded regions and planes
- Explore the use of computational tools like Wolfram Alpha for verifying integral calculations
USEFUL FOR
Students in calculus courses, particularly those focusing on multivariable calculus, as well as educators seeking to clarify the concepts of multiple integration and volume calculations in three-dimensional geometry.