Find work given two conservative forces and a nonconservative force

[bremenfallturm]

Homework Statement

A particle starts from rest in the point $A$ to the point $B$ along four different paths according to the figure (see my post):
1. A conservative force $F_{K1}$ does work $10J$ on the particle
2. A conservative force $F_{K2}$ does work $5$ on the particle
3. A nonconservative force $F_{IK}$ does work $-5J$ on the particle.
Now assume all forces act at the same time on the particle, when it is moved along the path 4. Find the work done by $F_{IK}$ given that the particle stops at point $B$

Relevant Equations

$U=\int_{\mathcal C} \vec F \cdot \vec dr$

$U=V(A)-V(B)$ if a force is conservative and $V$ is a potential function for it

$U=\oint_{\gamma} \vec F \cdot \vec dr$ for a closed curve $\gamma$

The figure provided with the question is:

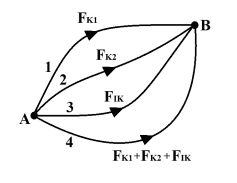
I set up the following equation for path 4
$U_{path 4}=U_{Fk1, path 4}+U_{Fk2, path 4}+U_{FIK, path 4}$ where $U_{FIK,AB}$ is the unknown.
I know that the work will be the same regardless the path for conservative forces, so I have:
$U_{path 4}=10+5+U_{FIK, path 4} (J)$
The answer key says $U_{FIK, path 4}=-15J$ (no further solution given), but I do not understand why $U_{path 4}$ is $0$, if I set up my equations correctly and interpret the answer key. I know that mechanical energy is conserved with conservative forces, and that the work done over a closed curve with conservative forces is 0.
How can I come to a reasoning that $-15J$ is correct?
Thanks!

 

[Orodruin]

Since the particle starts from rest and stops at B, the work-energy theorem requires the total work done on the particle is zero.

 

[kuruman]

Homework Statement: A particle starts from rest in the point $A$ to the point $B$ along four different paths according to the figure (see my post):
1. A conservative force $F_{K1}$ does work $10J$ on the particle
2. A conservative force $F_{K1}$ does work $10J$ on the particle
3. A nonconservative force $F_{IK}$ does work $-5J$ on the particle.

The work done by $F_{K1}$ is mentioned twice and the work done by $F_{K2}$ is not mentioned at all. Please specify.

 

[bremenfallturm]

The work done by $F_{K1}$ is mentioned twice and the work done by $F_{K2}$ is not mentioned at all. Please specify.

Megasuperdupersorry, copy paste let me down. I've clarified, see #1.

 

[kuruman]

Thank you for the clarification. You should cast the problem not in terms of potential energy changes because non-conservative forces cannot be derived from a potential energy function. Use the work-energy energy theorem approach as @Orodruin suggested in post #2. Note that

1. The total work done by the conservative forces is independent of path.
2. The work done by the non-conservative force along path 3 (= -5 J) is totally irrelevant to the answer.

 

[bremenfallturm]

Thank you for the clarification. You should cast the problem not in terms of potential energy changes because non-conservative forces cannot be derived from a potential energy function. Use the work-energy energy theorem approach as @Orodruin suggested in post #2. Note that

1. The total work done by the conservative forces is independent of path.
2. The work done by the non-conservative force along path 3 (= -5 J) is totally irrelevant to the answer.

Alright! So for path (4), we simply know that
$$U_{1-2}=\underbrace{\frac{1}{2}mv_b^2}_{=0}-\underbrace{\frac{1}{2}mv_a^2}_{=0}$$
$$\implies 0=5+10+U_{FIk, path 4}\implies U_{FIk, path 4}=-15 J$$

I think I missed the fact that the work-energy theorem applies to all forces, I don't know why I've thought the other way around, it seems obvious now when I think about it. With the reservation of this being a dumb question, for the other three paths we also start and end at rest, but there is not zero work. That's, what I assume, from other unknown forces acting on the particle. We assume that they don't do any work on it for path (4), since the work-energy theorem is for the sum of all forces, or did I misunderstand the concept of it?

 

[Orodruin]

for the other three paths we also start and end at rest

No we don't. There is no such statement in the problem.

 

[bremenfallturm]

No we don't. There is no such statement in the problem.

Hm, okay. You're right, I re-read the statement. It says that the particle "stops" at B in situation 4 and "moves" to B in the other scenarios. It was even clearer in the original problem statement, which is not in English so I had to translate it. Thank you, I think I get it now!

 

[bremenfallturm]

(Is there any way I can mark a thread as solved? Still new to this forum )

 

[kuruman]

(Is there any way I can mark a thread as solved? Still new to this forum )

We are not formal in that regard. Once the OP (original poster) provides a solution as you have in post #6, that’s it. Thank you for your contribution and do come back. We are here to help.