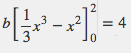Find x Coordinate of Point A for Maths Integration Area Problem

[MarkFL]

Here is the question:

Maths integration area problem?


The curve y = -3x(x − 2) where the area under the curve is 4 units² (0 ≤ x ≤ 2)

Find the x−coordinate of the point A if the line OA divides the shaded area into equal parts.
(function OA travels through the origin)

Could you show your solution with all steps


Additional Details:

Point A is located on the function y = -3x(x − 2)

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Phyllis,

Let's let the line passing through the origin be given by:

\(\displaystyle y=mx\)

We need to know where the line and the parabola intersect, hence equating the two, we find:

\(\displaystyle mx=-3x(x-2)\)

\(\displaystyle 3x^2+(m-6)x=0\)

\(\displaystyle x(3x+m-6)=0\)

We are interested in the point of intersection that is not the origin, so we look at:

\(\displaystyle 3x+m-6=0\)

\(\displaystyle x=\frac{6-m}{3}=2-\frac{m}{3}\)

Because the roots of the quadratic are $x=0,\,2$, we should expect to find $0<m<6$.

Now, we want to equate the area below the parabola and above the line to the area below the line and parabola. Thus, we should state:

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x^2+(6-m)x\,dx=m\int_0^{\frac{6-m}{3}}x\,dx-3\int_{\frac{6-m}{3}}^2 x^2-2x\,dx\)

Applying the FTOC, we obtain:

\(\displaystyle \left[-x^3+\frac{6-m}{2}x^2 \right]_0^{\frac{6-m}{3}}=\frac{m}{2}\left[x^2 \right]_0^{\frac{6-m}{3}}-3\left[\frac{1}{3}x^3-x^2 \right]_{\frac{6-m}{3}}^2\)

\(\displaystyle -\left(\frac{6-m}{3} \right)^3+\frac{6-m}{2}\left(\frac{6-m}{3} \right)^2=\frac{m}{2}\left(\frac{6-m}{3} \right)^2-3\left(\left(\frac{1}{3}2^3-2^2 \right)-\left(\frac{1}{3}\left(\frac{6-m}{3} \right)^3-\left(\frac{6-m}{3} \right)^2 \right) \right)\)

\(\displaystyle \left(\frac{6-m}{3} \right)^3=4\)

And so the $x$-coordinate of point $A$ is:

\(\displaystyle \frac{6-m}{3}=\sqrt[3]{4}\)

Here is a plot of the parabola and the line through the origin that divides the area under the parabola into two equal parts:

View attachment 1547

 

[Nemo1]

Hello Phyllis,

Let's let the line passing through the origin be given by:

\(\displaystyle y=mx\)

We need to know where the line and the parabola intersect, hence equating the two, we find:

\(\displaystyle mx=-3x(x-2)\)

\(\displaystyle 3x^2+(m-6)x=0\)

\(\displaystyle x(3x+m-6)=0\)

We are interested in the point of intersection that is not the origin, so we look at:

\(\displaystyle 3x+m-6=0\)

\(\displaystyle x=\frac{6-m}{3}=2-\frac{m}{3}\)

Because the roots of the quadratic are $x=0,\,2$, we should expect to find $0<m<6$.

Now, we want to equate the area below the parabola and above the line to the area below the line and parabola. Thus, we should state:

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x^2+(6-m)x\,dx=m\int_0^{\frac{6-m}{3}}x\,dx-3\int_{\frac{6-m}{3}}^2 x^2-2x\,dx\)

Applying the FTOC, we obtain:

\(\displaystyle \left[-x^3+\frac{6-m}{2}x^2 \right]_0^{\frac{6-m}{3}}=\frac{m}{2}\left[x^2 \right]_0^{\frac{6-m}{3}}-3\left[\frac{1}{3}x^3-x^2 \right]_{\frac{6-m}{3}}^2\)

\(\displaystyle -\left(\frac{6-m}{3} \right)^3+\frac{6-m}{2}\left(\frac{6-m}{3} \right)^2=\frac{m}{2}\left(\frac{6-m}{3} \right)^2-3\left(\left(\frac{1}{3}2^3-2^2 \right)-\left(\frac{1}{3}\left(\frac{6-m}{3} \right)^3-\left(\frac{6-m}{3} \right)^2 \right) \right)\)

\(\displaystyle \left(\frac{6-m}{3} \right)^3=4\)

And so the $x$-coordinate of point $A$ is:

\(\displaystyle \frac{6-m}{3}=\sqrt[3]{4}\)

Here is a plot of the parabola and the line through the origin that divides the area under the parabola into two equal parts:

In Phyllis's question she started with y=-3x(x-2)

If I had y=bx(x-2) and had to solve for b how does it become b=-3?

Many thanks in advance.

 

[MarkFL]

In Phyllis's question she started with y=-3x(x-2)

If I had y=bx(x-2) and had to solve for b how does it become b=-3?

Many thanks in advance.

If we have:

\(\displaystyle y=bx(x-2)\)

And we require the area under the curve and above the $x$-axis to be 4, then we could state:

\(\displaystyle \int_0^2 bx(x-2)\,dx=4\)

Expand the integrand:

\(\displaystyle b\int_0^2 x^2-2x\,dx=4\)

Apply the FTOC:

\(\displaystyle b\left[\frac{1}{3}x^3-x^2\right]_0^2=4\)

\(\displaystyle b\left(\frac{8}{3}-4\right)=4\)

\(\displaystyle b\left(\frac{2}{3}-1\right)=1\)

\(\displaystyle -\frac{1}{3}b=1\)

\(\displaystyle b=-3\)

 

[Nemo1]

Hi MarkFL,

Thanks for the detailed answer, I was wondering how it moves from

View attachment 4993

To

View attachment 4994

I see that the x term has been removed but I am unsure of how to do it.

The rest I understand to solve for b.

Thanks and much appreciated!

 

[MarkFL]

The anti-derivative form of the FTOC states:

\(\displaystyle \int_a^b f(x)\,dx=F(b)-F(a)\) where \(\displaystyle \d{F}{x}=f(x)\)

In our case, we have:

\(\displaystyle f(x)=x^2-2x\implies F(x)=\frac{1}{3}x^3-x^2\)

Since $F(0)=0$, we simply have:

\(\displaystyle \int_0^2 f(x)\,dx=F(2)\)...does this clear things up? :)

 

[Nemo1]

Hi MarkFL,

I see how to take the anti-derivative in your explanation but I am still missing how it became

View attachment 4995

with the x term removed.

Thanks heaps for your time.

 

[MarkFL]

Given:

\(\displaystyle F(x)=\frac{1}{3}x^3-x^2\)

then what is $F(2)$?

 

[Nemo1]

Hi Mark,

Light bulb moment, thanks.

 

[Nemo1]

Hi MarkFL,

In the graph

View attachment 4997

How do you find the slope of the line that passes thru the point A which I understand its x coordinate is the cube root of 4.

I am unsure of how to find the y coordinate too

I really appreciate your help in helping me understand this.

 

[MarkFL]

Hi MarkFL,

In the graph
How do you find the slope of the line that passes thru the point A which I understand its x coordinate is the cube root of 4.

I am unsure of how to find the y coordinate too

I really appreciate your help in helping me understand this.

You did you determine the $y$-coordinate of point $A$ is 2? If I wanted to find the slope of the line, I would take the equation:

\(\displaystyle \frac{6-m}{3}=\sqrt[3]{4}\)

and solve for $m$.

edit: you edited your post...

 

[Nemo1]

Hi MarkFL,

When I solve for m I get

View attachment 4999

When I put this into Wolfram as the slope it tells me the intercept with the original equation y=-3x(x-2)

is

View attachment 5000

Which is approx 1.964880012

I graphed this in Grapher on my Mac and it confirms this visually for me but I don't understand why its not equal to 2
Below is the screen shot of the graph all intersecting at point A
View attachment 5001Again, many thanks for you time.

 

[MarkFL]

...but I don't understand why its not equal to 2...

What makes you think the $y$-coordinate of $A$ should be 2?

 

[Nemo1]

Hi MarkFL,

From you comment of "You did you determine the $y$-coordinate of point $A$ is 2?"

I was interpreting this as the y coord of $A$=2

Quote: You did you determine the $y$-coordinate of point $A$ is 2? If I wanted to find the slope of the line, I would take the equation:

\(\displaystyle \frac{6-m}{3}=\sqrt[3]{4}\)

and solve for $m$.

How would I solve for $A$ y coord?

Thanks for your awesome help.

 

[MarkFL]

I was simply curious how you made that earlier determination, because I knew it was incorrect.

We know:

\(\displaystyle m=6-3\sqrt[3]{4}\)

And so the $y$-coordinate of point $A$ would be:

\(\displaystyle \left(6-3\sqrt[3]{4}\right)\sqrt[3]{4}=6\sqrt[3]{2}\left(\sqrt[3]{2}-1\right)\approx1.96488\)

This is what you correctly found. :D

 

[Nemo1]

Hi MarkFL,

Thanks for your last answer, it helps.

Can I take a few steps back and ask a bit more on creating the definite integral. (Please correct my terminology if I am wrong)

I want to understand the process to be able to apply this knowledge and I thank you so much for your help so far.

I understand that \(\displaystyle mx=-3x(x-2)\) becomes \(\displaystyle -3x(x-2)-mx\) by subtracting \(\displaystyle -mx\) from both sides.

So now with the formula \(\displaystyle -3x(x-2)-mx\) my understanding is that we plug the anti derivatives into a definite integral where the lower boundary is zero and the upper is \(\displaystyle {\frac{6-m}{3}}\)

If we use the FTOC \(\displaystyle \int_{a}^{b} \, f(x) dx = F(b)- F(a)\,dx\)

I see that \(\displaystyle f(x) dx\) becomes \(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx\) = \(\displaystyle F(b)- F(a)\,dx\)

to get \(\displaystyle F(b)- F(a)\,dx\) you have split the definite integral into two sections to get \(\displaystyle \int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

by moving mx to its own definite integral of \(\displaystyle \int_0^{\frac{6-m}{3}}mx\,dx\) added to \(\displaystyle \int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

Can you please clarify why the \(\displaystyle -mx\) lost it negative sign?

Am I right in saying that by moving \(\displaystyle mx\) to its own definite integral we are saying that \(\displaystyle F(b)\) is \(\displaystyle \int_0^{\frac{6-m}{3}}mx\,dx\)

Then it is added to \(\displaystyle \int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\) which is \(\displaystyle F(a)\,dx\)

This then gives us the full domain along x from \(\displaystyle 0\) to \(\displaystyle {\frac{6-m}{3}}\) to 2

Put together then gives us \(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\) which is now in the correct format of \(\displaystyle \int_{a}^{b} \, f(x) dx = F(b)- F(a)\,dx\)

Next,

On the simplification of \(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

How did \(\displaystyle -3x(x-2)-mx\) become \(\displaystyle -3x^2+(6-m)x\) and not \(\displaystyle -3x^3+6x^2-mx\) when expanded?
I can see that you have moved the constants (please correct me if its wrong to call them that) \(\displaystyle m\) & \(\displaystyle -3\) in front of the definite integral.

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)
\(\displaystyle \int_0^{\frac{6-m}{3}} -3x^2+(6-m)x\,dx=m\int_0^{\frac{6-m}{3}}x\,dx-3\int_{\frac{6-m}{3}}^2 x^2-2x\,dx\)

Then taken the integrals of:
\(\displaystyle -3x^2\) = \(\displaystyle -x^3\)
\(\displaystyle (6-m)\) = \(\displaystyle \frac{6-m}{2}\)
\(\displaystyle x\) = \(\displaystyle x^2\)
\(\displaystyle x^2\) = \(\displaystyle \frac{1}{3}x^3\)

To then get

\(\displaystyle \left[-x^3+\frac{6-m}{2}x^2 \right]_0^{\frac{6-m}{3}}=\frac{m}{2}\left[x^2 \right]_0^{\frac{6-m}{3}}-3\left[\frac{1}{3}x^3-x^2 \right]_{\frac{6-m}{3}}^2\)

Now we can plug in our \(\displaystyle x={\frac{6-m}{3}}\) in every x in the above to get.\(\displaystyle -\left(\frac{6-m}{3} \right)^3+\frac{6-m}{2}\left(\frac{6-m}{3} \right)^2=\frac{m}{2}\left(\frac{6-m}{3} \right)^2-3\left(\left(\frac{1}{3}2^3-2^2 \right)-\left(\frac{1}{3}\left(\frac{6-m}{3} \right)^3-\left(\frac{6-m}{3} \right)^2 \right) \right)\)

I am unsure of how the above becomes

\(\displaystyle \left(\frac{6-m}{3} \right)^3=4\)

I understand to get \(\displaystyle \frac{6-m}{3}=\sqrt[3]{4}\) you took the cube root of both sides of \(\displaystyle \left(\frac{6-m}{3} \right)^3=4\)

So now I understand that \(\displaystyle x=\sqrt[3]{4}\) and previously we found that \(\displaystyle m=6-3\sqrt[3]{4}\)

Put together into Slope intercept form \(\displaystyle y=mx+b\) we get \(\displaystyle y=6-3\sqrt[3]{4}\cdot\sqrt[3]{4}+0\) to find the \(\displaystyle y\) coordinate of point \(\displaystyle A\) on the curve \(\displaystyle y=-3x(x-2)\) which \(\displaystyle \approx1.96488\)

I hope I have clearly expressed where my confusion is and that you are able to fill in the gaps, as I said I really want to understand this.

 

[MarkFL]

Hi MarkFL,

Thanks for your last answer, it helps.

You're welcome and please...just call me Mark. :)

Can I take a few steps back and ask a bit more on creating the definite integral. (Please correct my terminology if I am wrong)

I want to understand the process to be able to apply this knowledge and I thank you so much for your help so far.

I understand that \(\displaystyle mx=-3x(x-2)\) becomes \(\displaystyle -3x(x-2)-mx\) by subtracting \(\displaystyle -mx\) from both sides.

To be precise, I took:

\(\displaystyle mx=-3x(x-2)\)

added $-3x(x-2)$ to both sides to get:

\(\displaystyle 3x^2+(m-6)x=0\)

and then factored to obtain:

\(\displaystyle x(3x+m-6)=0\)

Since we know both the dividing line and the parabola pass through the origin, we discard the root $x=0$, and focus solely on the root obtain from:

\(\displaystyle 3x+m-6=0\)

to obtain:

\(\displaystyle x=\frac{6-m}{3}=2-\frac{m}{3}\)

So now with the formula \(\displaystyle -3x(x-2)-mx\) my understanding is that we plug the anti derivatives into a definite integral where the lower boundary is zero and the upper is \(\displaystyle {\frac{6-m}{3}}\)

If we use the FTOC \(\displaystyle \int_{a}^{b} \, f(x) dx = F(b)- F(a)\,dx\)

I want to pause here, to say that the correct statement of the anti-derivative form of the FTOC is:

\(\displaystyle \int_a^b f(x)\,dx=F(b)-F(a)\)

You have included a differential on the right side that doesn't belong there.

I see that \(\displaystyle f(x) dx\) becomes \(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx\) = \(\displaystyle F(b)- F(a)\,dx\)

to get \(\displaystyle F(b)- F(a)\,dx\) you have split the definite integral into two sections to get \(\displaystyle \int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

by moving mx to its own definite integral of \(\displaystyle \int_0^{\frac{6-m}{3}}mx\,dx\) added to \(\displaystyle \int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

Can you please clarify why the \(\displaystyle -mx\) lost it negative sign?

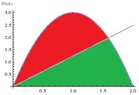
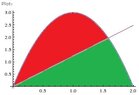
What I did next was to equate the area in red (below the parabola and above the line) to the area in green (the area under the line and under the parabola). Recall that to find the area bounded by two functions, we take the upper function minus the lower function on the given interval. In the case of the red area, the upper function is the parabola, and the lower function is the line. And so the area red can be written as:

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx\)

Now the green area is a bit more complicated since for part of the area the line is the upper function and the $x$-axis is the lower function and for the remaining part, the parabola is the upper function and the $x$-axis is the lower function. And so it's area is given by:

\(\displaystyle \int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

And because we require that these areas be equal, we then equate them:

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

So, as you see, on the left within the integrand the term $mx$ has a negative sign because it is the lower function and is being subtracted from the upper function, while on the right it has a positive sign because it is the upper function.

Am I right in saying that by moving \(\displaystyle mx\) to its own definite integral we are saying that \(\displaystyle F(b)\) is \(\displaystyle \int_0^{\frac{6-m}{3}}mx\,dx\)

Then it is added to \(\displaystyle \int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\) which is \(\displaystyle F(a)\,dx\)

This then gives us the full domain along x from \(\displaystyle 0\) to \(\displaystyle {\frac{6-m}{3}}\) to 2

Put together then gives us \(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\) which is now in the correct format of \(\displaystyle \int_{a}^{b} \, f(x) dx = F(b)- F(a)\,dx\)

I am hoping any questions here have been addressed above.

Next,

On the simplification of \(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

How did \(\displaystyle -3x(x-2)-mx\) become \(\displaystyle -3x^2+(6-m)x\) and not \(\displaystyle -3x^3+6x^2-mx\) when expanded?

Let's look at:

\(\displaystyle -3x(x-2)-mx\)

Distribute $-3x$:

\(\displaystyle -3x^2+6x-mx\)

Factor on like powers of $x$:

\(\displaystyle -3x^2+(6-m)x\)

I can see that you have moved the constants (please correct me if its wrong to call them that) \(\displaystyle m\) & \(\displaystyle -3\) in front of the definite integral.

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x(x-2)-mx\,dx=\int_0^{\frac{6-m}{3}}mx\,dx+\int_{\frac{6-m}{3}}^2 -3x(x-2)\,dx\)

\(\displaystyle \int_0^{\frac{6-m}{3}} -3x^2+(6-m)x\,dx=m\int_0^{\frac{6-m}{3}}x\,dx-3\int_{\frac{6-m}{3}}^2 x^2-2x\,dx\)

Yes, any constant factors of an integrand can be factored out in from of the integral.

Then taken the integrals of:
\(\displaystyle -3x^2\) = \(\displaystyle -x^3\)
\(\displaystyle (6-m)\) = \(\displaystyle \frac{6-m}{2}\)
\(\displaystyle x\) = \(\displaystyle x^2\)
\(\displaystyle x^2\) = \(\displaystyle \frac{1}{3}x^3\)

The second term is actually:

\(\displaystyle (6-m)x\)

and then integrating, we obtain:

\(\displaystyle (6-m)\frac{x^2}{2}=\frac{6-m}{2}x^2\)

To then get

\(\displaystyle \left[-x^3+\frac{6-m}{2}x^2 \right]_0^{\frac{6-m}{3}}=\frac{m}{2}\left[x^2 \right]_0^{\frac{6-m}{3}}-3\left[\frac{1}{3}x^3-x^2 \right]_{\frac{6-m}{3}}^2\)

Now we can plug in our \(\displaystyle x={\frac{6-m}{3}}\) in every x in the above to get.

To be clear, the notation:

\(\displaystyle \left[g(x)\right]_a^b=g(b)-g(a)\)

\(\displaystyle -\left(\frac{6-m}{3} \right)^3+\frac{6-m}{2}\left(\frac{6-m}{3} \right)^2=\frac{m}{2}\left(\frac{6-m}{3} \right)^2-3\left(\left(\frac{1}{3}2^3-2^2 \right)-\left(\frac{1}{3}\left(\frac{6-m}{3} \right)^3-\left(\frac{6-m}{3} \right)^2 \right) \right)\)

I am unsure of how the above becomes

\(\displaystyle \left(\frac{6-m}{3} \right)^3=4\)

Let's look at the left side:

\(\displaystyle -\left(\frac{6-m}{3} \right)^3+\frac{6-m}{2}\left(\frac{6-m}{3}\right)^2\)

We see that both terms have \(\displaystyle \frac{(6-m)^3}{9}\) as a factor, so we may factor this as:

\(\displaystyle \frac{(6-m)^3}{9}\left(-\frac{1}{3}+\frac{1}{2}\right)\)

And combining terms within the parentheses, we obtain:

\(\displaystyle \frac{(6-m)^3}{54}\)

Now let's look at the right side:

\(\displaystyle \frac{m}{2}\left(\frac{6-m}{3}\right)^2-3\left(\left(\frac{1}{3}2^3-2^2\right)-\left(\frac{1}{3}\left(\frac{6-m}{3}\right)^3-\left(\frac{6-m}{3}\right)^2 \right)\right)\)

In the second term, let's simplify:

\(\displaystyle \frac{m}{2}\left(\frac{6-m}{3}\right)^2-3\left(\left(\frac{8}{3}-4\right)-\left(\frac{6-m}{3}\right)^2\left(\frac{6-m}{9}-1\right)\right)\)

\(\displaystyle \frac{m}{2}\left(\frac{6-m}{3}\right)^2+3\left(\frac{4}{3}+\left(\frac{6-m}{3}\right)^2\left(\frac{6-m}{9}-1\right)\right)\)

\(\displaystyle \frac{m}{2}\left(\frac{6-m}{3}\right)^2+4+\left(\frac{6-m}{3}\right)^2\left(\frac{6-m}{3}-3\right)\)

\(\displaystyle \frac{m}{2}\left(\frac{6-m}{3}\right)^2+4+\left(\frac{6-m}{3}\right)^3-3\left(\frac{6-m}{3}\right)^2\)

Now, equating the two simplified sides, we have:

\(\displaystyle \frac{(6-m)^3}{54}=\frac{m}{2}\left(\frac{6-m}{3}\right)^2+4+\left(\frac{6-m}{3}\right)^3-3\left(\frac{6-m}{3}\right)^2\)

We can then arrange this as:

\(\displaystyle \frac{(6-m)^3}{54}-\frac{m}{2}\left(\frac{6-m}{3}\right)^2-\left(\frac{6-m}{3}\right)^3+3\left(\frac{6-m}{3}\right)^2=4\)

Factor:

\(\displaystyle \left(\frac{6-m}{3}\right)^2\left(\frac{6-m}{6}-\frac{m}{2}-\frac{6-m}{3}+3\right)=4\)

Simplify:

\(\displaystyle \left(\frac{6-m}{3}\right)^2\left(\frac{6-m-3m-12+2m+18}{6}\right)=4\)

\(\displaystyle \left(\frac{6-m}{3}\right)^2\left(\frac{12-2m}{6}\right)=4\)

\(\displaystyle \left(\frac{6-m}{3}\right)^2\left(\frac{6-m}{3}\right)=4\)

\(\displaystyle \left(\frac{6-m}{3}\right)^3=4\)

I understand to get \(\displaystyle \frac{6-m}{3}=\sqrt[3]{4}\) you took the cube root of both sides of \(\displaystyle \left(\frac{6-m}{3} \right)^3=4\)

So now I understand that \(\displaystyle x=\sqrt[3]{4}\) and previously we found that \(\displaystyle m=6-3\sqrt[3]{4}\)

Put together into Slope intercept form \(\displaystyle y=mx+b\) we get \(\displaystyle y=6-3\sqrt[3]{4}\cdot\sqrt[3]{4}+0\) to find the \(\displaystyle y\) coordinate of point \(\displaystyle A\) on the curve \(\displaystyle y=-3x(x-2)\) which \(\displaystyle \approx1.96488\)

I hope I have clearly expressed where my confusion is and that you are able to fill in the gaps, as I said I really want to understand this.

Yes, that's correct. :D

 

[Nemo1]

Hi Mark,

Thank you for breaking it down in a way that I could understand.

Many many thanks for your time in helping me to understand better the fundamental theorem of calculus and factoring.

Cheers Nemo.