lucasLima
- 17
- 0
Hi Guys, that's what i got
<x,z>=<y,z>
<x,z>-<y,z>=0
<x,z>+<-y,z>=0
<x-y,z>=0
x-y = [0,2,0]
<2*[0,1,0],Z>=0
2<[0,1,0],z> = 0
<[0,1,0],z>=0
So 'im stuck at that. Any ideas?
The discussion focuses on solving the equation system involving vectors where the inner products
Mathematicians, physics students, and anyone involved in vector analysis or linear algebra who seeks to deepen their understanding of vector relationships and inner product properties.
If you write z with its components, what do you get as result?lucasLima said:<[0,1,0],z>=0
mfb said:If you write z with its components, what do you get as result?
Unrelated:
You didn't use the "=0" part yet.
mfb said:Well, it is the first part of the solution, yes.
One thing I don't see mentioned in this thread is that the notation <x, z> represents the inner product of x and z, I believe. If z is an arbitrary vector with z = <z1, z2, z3>, then <x, z> = 0 means that x and z are perpendicular. Also, <x, z> = ##x_1z_1 + x_2z_2 + x_3z_3 = z_1 + z_2 + z_3##, and similarly for <y, z>.lucasLima said: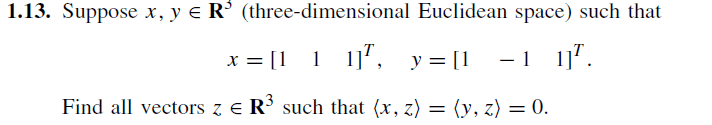
Hi Guys, that's what i got
<x,z>=<y,z>
<x,z>-<y,z>=0
<x,z>+<-y,z>=0
<x-y,z>=0
x-y = [0,2,0]
<2*[0,1,0],Z>=0
2<[0,1,0],z> = 0
<[0,1,0],z>=0
So 'im stuck at that. Any ideas?