Finding asymptotes of parametric equations

[fluppocinonys]

Find the asymptotes of the parametric equations

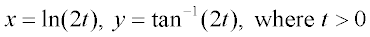
The graph looks like this:

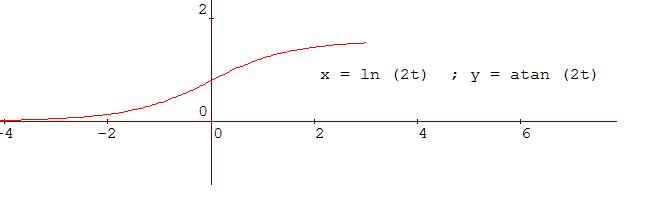
My attempt:

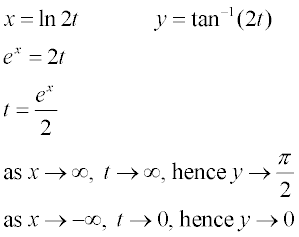
Is my presentation correct? Do I also need to consider as x approaches 0 ?



The reasons I ask is because I couldn't find the asymptotes of

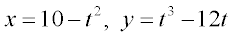
if I use the above presentation...
Please guide me...
Thanks.

 

[Mark44]

The first problem looks fine, although you could have done it without solving for t in the first equation. Just look at what happens to x and y as x gets large or approaches zero. If x = 0, y = pi/4. All this is, is the y-intercept.

For the second problem, there aren't any asymptotes. As x --> infinity, x --> -infinity and y --> +infinity. As x --> -infinity, x --> -infinity and y --> -infinity. For intercepts, set x = 0 and solve for t, then substitute it into the other equation. That will give you the y-intercept(s). Set y = 0 and solve for t, then substitute it into the other equation, to get the x-intercepts(s).