Finding charge on a capacitor given potential difference across two points

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

Please see below

For this part(b) of this problem,

The solution is

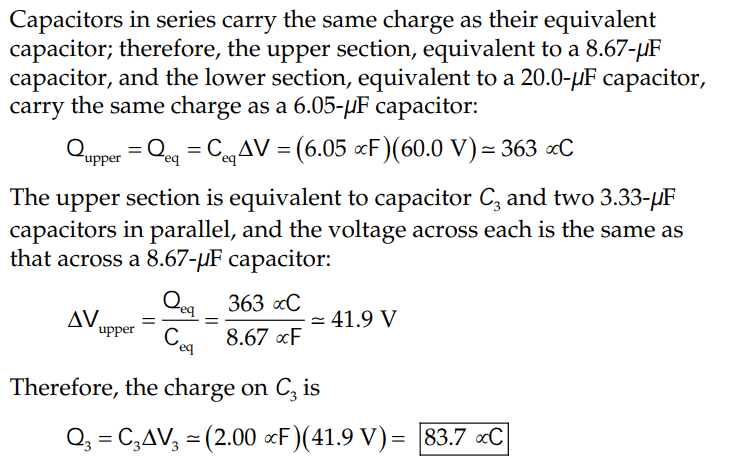
However, I tried solving (b) like this:

Since $Q_{total} = 363 \times 10^{-6} C$ then $Q_1 = 181.5 \times 10^{-6} C$ since the equivalent upper capacitor is in series with the equivalent bottom capacitor so should store the same amount of charge.

Since $C_{upper} = 8.67 \times 10^{-6} C$ then voltage across upper equivalent capacitor is $\frac {181.5}{8.67} = 21V$ then charged stored by $C_3$ is $Q_3 = 2 \times 10^{6} \times 21 = 4.2 \times 10^{-5}$

I don't understand why they use the total charge for the upper capacitors when they only store half the charge.
Many thanks!

 

[nasu]

What do you label as Q₁?

 

[ChiralSuperfields]

What do you label as Q₁?

Thank you for your reply @nasu!

I'm not sure, just some notation for the upper equivalent capacitors charge.

 

[nasu]

Then this is already labeled as Q _total. This is the charge on the upper group of capacitors. And the same charge is on the lower group, which is in series with the upper group.
.

 

[ChiralSuperfields]

Then this is already labeled as Q _total. This is the charge on the upper group of capacitors. And the same charge is on the lower group, which is in series with the upper group.
.

Thank you for your reply @nasu! I forgot capacitor in series have the same charge!